Summary
| 시간복잡도 | 평균 \(O(n log n)\), 최악 \(O(n^2)\) |
| 공간복잡도 | \(O(n)\) |
| 정렬 특징 | 불안정 정렬 |
특징
- 분할 정복
- 재귀
Details
메소드 구성
QuickSort(arr, left, right)
- 배열의
left~right인덱스 내에서만 정렬을 수행한다.
Partition(arr, left, right)
- 배열의
left~right인덱스 내에서 피벗을 선정한다. - 내부적으로 정렬을 수행하고, 피벗의 인덱스를 리턴한다.
정렬 과정
[1] QuickSort(arr, 0, arr.Length - 1)를 통해 정렬을 시작한다.

[2] Partition(arr, left, right) 메소드를 통해 left ~ right 범위 내에서 피벗을 선정한다.

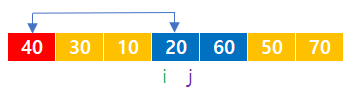
[3-1] j 인덱스는 right 인덱스에서 출발하여 좌측으로 이동하며, pivot이 위치한 값보다 작거나 같은 값을 찾는다.
[3-2] i 인덱스는 left + 1 인덱스에서 출발하여 우측으로 이동하며, pivot이 위치한 값보다 큰 값을 찾는다.

[3-3] i와 j 위치의 값을 서로 바꾼다.

[4] i < j인 동안 [3-1], [3-2], [3-3]을 반복한다.

[5] i >=j인 경우, i 인덱스와 pivot 인덱스의 값을 서로 바꾼다.
[6] Partition(..) 메소드는 최종적으로 i 인덱스를 리턴한다.

[7] Partition(..) 메소드를 통해 얻은 값을 pivot이라고 할 때, 재귀적으로 QuickSort(arr, left, pivot - 1), QuickSort(arr, pivot + 1, right)를 반복한다.

[8] left >= right인 경우, 재귀를 종료한다.

시간복잡도
-
pivot을 최솟값 또는 최댓값으로 선정하는 경우 최악의 시간복잡도인 \(O(n^2)\)에 해당한다. -
pivot을 중간값으로 선정하는 경우 \(O(nlogn)\)에 해당한다. -
따라서
pivot을 선정하는 방법에 따라 효율성이 결정될 수 있다.
Source Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public static void QuickSort(int[] array)
{
QuickSortInternal(array, 0, array.Length - 1);
}
public static void QuickSortInternal(int[] array, int left, int right)
{
if(left >= right) return;
int pivot = Partition(array, left, right);
QuickSortInternal(array, left, pivot - 1);
QuickSortInternal(array, pivot + 1, right);
}
public static int Partition(int[] array, int left, int right)
{
int i = left + 1, j = right;
int pivotValue = array[left];
while (i < j)
{
while(array[j] > pivotValue)
j--;
while(array[i] <= pivotValue && i < j)
i++;
Swap(array, i, j);
}
Swap(array, left, i);
return i;
}
/// <summary> 배열의 인덱스 i와 j 위치의 값 서로 변경 </summary>
public static void Swap<T>(T[] array, int i, int j)
{
T temp = array[i];
array[i] = array[j];
array[j] = temp;
}