Summary
직선을 그릴 때 직선 위의 점들은 실수 값을 가질 수밖에 없다.
그래서 불연속 정수 값만을 갖는 픽셀에 직선을 그릴 때는
실수 값의 소수점을 버리거나 반올림하여 정수로 변환해야 하는데,
브레즌햄 알고리즘은 실수 연산 없이 정수 연산만으로 직선을 그릴 수 있게 해준다.
Details
2가지 경우로 나눈다.
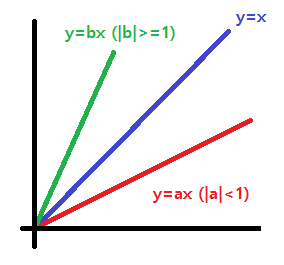
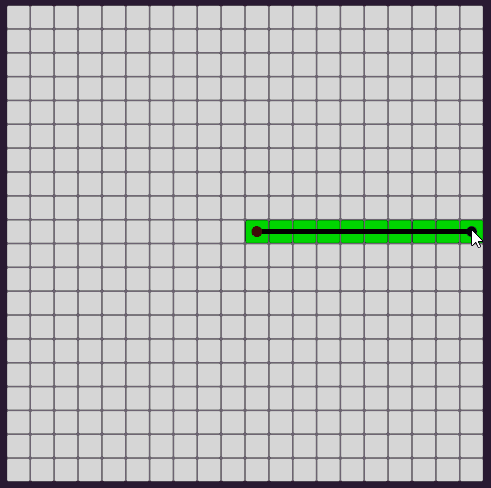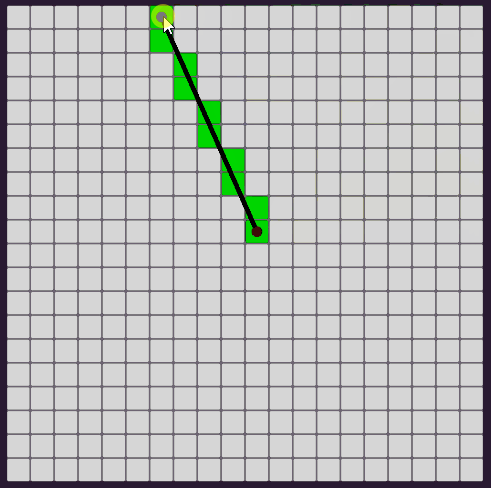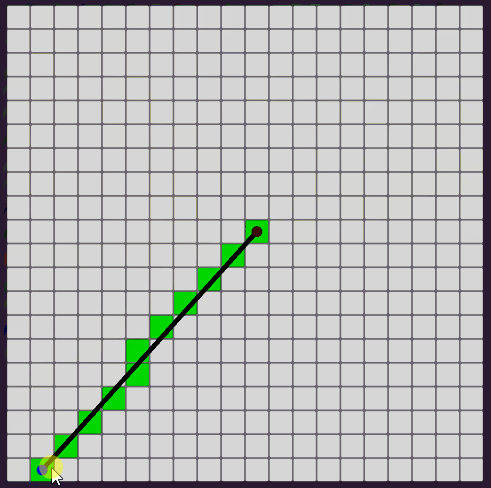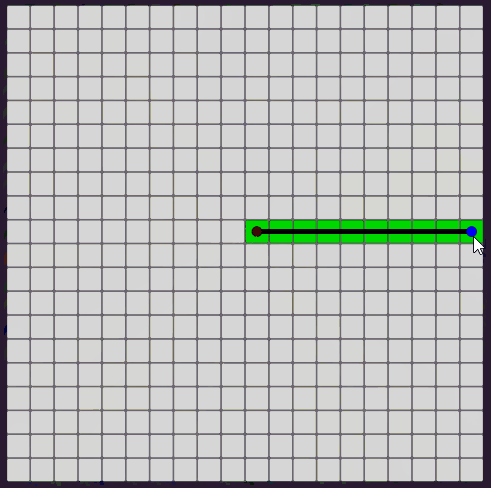
- 기울기 절댓값이 1 미만인 경우
- 기울기 절댓값이 1 이상인 경우
1번의 경우에는 x 좌표를 1씩 증가 또는 감소시키며 해당하는 y 좌표를 구하고,
2번의 경우에는 y 좌표를 1씩 증가 또는 감소시키며 해당하는 x 좌표를 구한다.
1번을 예시로 했을 때
x 좌표를 1씩 증가 또는 감소시켰을 때 y좌표 역시 1 증가 또는 감소시킬지 여부를 결정해야 하는데,
이를 판별값을 통해 계산한다.
직선을 그리기 위한 두 점을 각각 p1, p2,
w = p2.x - p1.x, h = p2.y - p1.y라고 한다.
판별값을 k라고 했을 때 다음 판별값을 계산하기 위한 두 가지 값을 각각 kA, kB라고 하며
k의 초깃값은 2|h| - |w|, kA와 kB의 값은 각각 2|h|, 2(|h| - |w|)이다.
x, y의 부호값(1, 0, -1)을 각각 sx, sy라고 한다.
Pseudo Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Point p1, p2
w = p2.x - p1.x
h = p2.y - p1.y
sx = Sign(w) // w의 부호값
sy = Sign(h) // h의 부호값
k = 2 * |h| - |w|
kA = 2 * |h|
kB = 2 * (|h| - |w|)
y = p1.y
for x = p1.x ~ p2.x; x += sx
DrawPoint(x, y)
if k < 0
k += kA
else
k += kB
y += sy
2번의 경우에는 1번에서 x, y를 서로 바꾸고 판별값에서 |h|, |w|를 서로 바꾸어 계산한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Point p1, p2
w = p2.x - p1.x
h = p2.y - p1.y
sx = Sign(w) // w의 부호값
sy = Sign(h) // h의 부호값
k = 2 * |w| - |h|
kA = 2 * |w|
kB = 2 * (|w| - |h|)
x = p1.x
for y = p1.y ~ p2.y; y += sy
DrawPoint(x, y)
if k < 0
k += kA
else
k += kB
x += sx
Source Code
Source Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
public struct Point
{
public int x;
public int y;
public Point(int x, int y)
{
this.x = x;
this.y = y;
}
public static implicit operator Point((int x, int y) p) => new Point(p.x, p.y);
public static bool operator ==(Point a, Point b) => a.x == b.x && a.y == b.y;
public static bool operator !=(Point a, Point b) => !(a.x == b.x && a.y == b.y);
public override string ToString() => $"({x}, {y})";
}
internal class Bresenham : IEnumerable
{
private readonly List<Point> points;
public int Count { get; private set; }
public Point this[int index]
{
get => points[index];
}
public Bresenham(Point p1, Point p2)
{
int w = Math.Abs(p2.x - p1.x);
int h = Math.Abs(p2.y - p1.y);
points = new List<Point>(w + h);
SetPoints(p1, p2);
Count = points.Count;
}
private void SetPoints(in Point p1, in Point p2)
{
int W = p2.x - p1.x; // width
int H = p2.y - p1.y; // height;
int absW = Math.Abs(W);
int absH = Math.Abs(H);
int xSign = Math.Sign(W);
int ySign = Math.Sign(H);
// 기울기 절댓값
float absM = (W == 0) ? float.MaxValue : (float)absH / absW;
int k; // 판별값
int kA; // p가 0 이상일 때 p에 더할 값
int kB; // p가 0 미만일 때 p에 더할 값
int x = p1.x;
int y = p1.y;
// 1. 기울기 절댓값이 1 미만인 경우 => x 기준
if (absM < 1f)
{
k = 2 * absH - absW; // p의 초깃값
kA = 2 * absH;
kB = 2 * (absH - absW);
for (; W >= 0 ? x <= p2.x : x >= p2.x; x += xSign)
{
points.Add((x, y));
if (k < 0)
{
k += kA;
}
else
{
k += kB;
y += ySign;
}
}
}
// 기울기 절댓값이 1 이상인 경우 => y 기준
else
{
k = 2 * absW - absH; // p의 초깃값
kA = 2 * absW;
kB = 2 * (absW - absH);
for (; H >= 0 ? y <= p2.y : y >= p2.y; y += ySign)
{
points.Add((x, y));
if (k < 0)
{
k += kA;
}
else
{
k += kB;
x += xSign;
}
}
}
}
public IEnumerator GetEnumerator()
{
return points.GetEnumerator();
}
}
Example - Unity