1. Original Fisher-Yates Shuffle
알고리즘
…

길이 n인 배열이 있다.
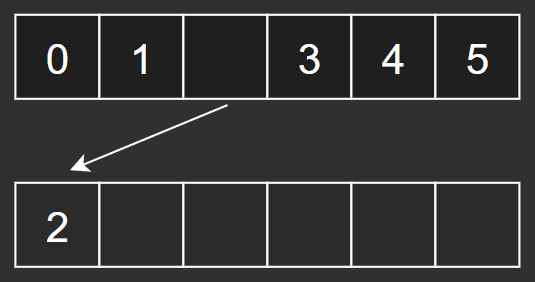
[0, n-1] 범위에서 무작위 인덱스를 뽑아, 그 위치의 원소를 새로운 배열의 인덱스 0 위치에 넣는다.
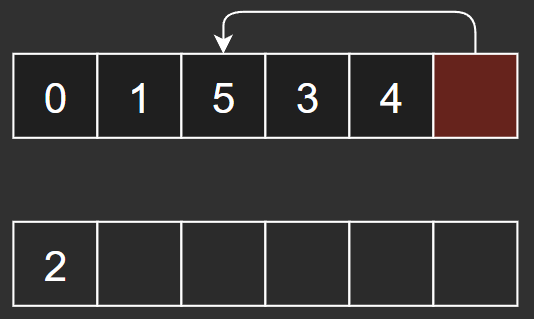
기존 배열에서 n-1 인덱스에 있는 원소를 구멍 뚫린 위치에 채워 넣는다.
뒤에서 한 칸씩 밀어서 빈 칸을 채우는 방법도 있겠으나, 그러면 O(n)에 해당하므로 정말 굉장히 비효율적이다.
끝에서 꺼내어 채워 넣으면 O(1)이므로 쓸만하다.
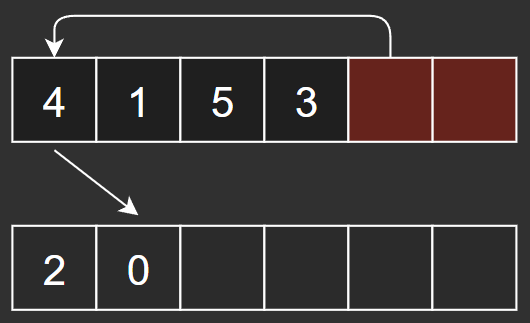
이번에는 [0, n-2] 범위에서 무작위 인덱스를 뽑아 새로운 배열의 인덱스 1에 넣고,
마찬가지로 n-2 인덱스의 원소를 구멍 뚫린 위치에 채워 넣는다.
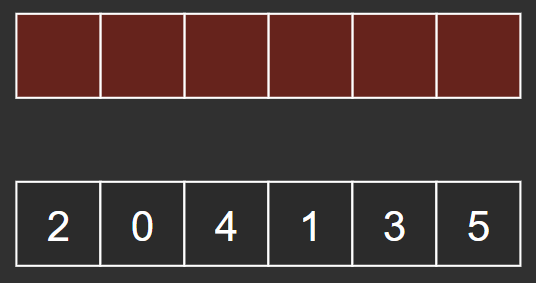
새로운 배열을 모두 채울 때까지 반복하면 된다.
단점
- 기존 배열 크기만큼의 새로운 배열이 필요하다.
소스 코드(C#)
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
private static System.Random random = new System.Random();
// Original Fisher-Yates Shuffle
private void Shuffle<T>(ref T[] array)
{
int n = array.Length;
T[] newArray = new T[n];
for(int i = 0; i < n; i++)
{
// 현재 배열 내에서 셔플되지 않은 원소들 중 마지막 원소의 인덱스
int last = n - 1 - i;
// 1. 무작위 위치의 원소를 새로운 배열에 차곡차곡 넣기
int r = random.Next(0, last + 1); // [0, n - 1 - i]
newArray[i] = array[r];
// 2. 기존 배열 빈칸 채우기
array[r] = array[last];
}
array = newArray;
}
2. Modern Fisher-Yates Shuffle
알고리즘
…

길이 n인 배열이 있다.
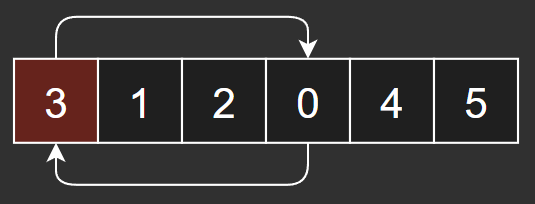
[0, n-1] 범위에서 무작위 인덱스를 뽑아, 그 원소를 인덱스 0에 위치한 원소와 서로 바꾼다.
[1, n-1]이 아니라 자기 자신을 포함하는 [0, n-1] 범위에서 뽑아, 위치가 바뀌지 않는 경우의 수도 포함하도록 한다.

다음에는 [1, n-1] 범위에서 무작위 인덱스를 뽑고, 그 원소를 인덱스 1에 위치한 원소와 서로 바꾼다.

[i, n-1] 인덱스 범위의 무작위 원소와 인덱스 i 의 원소를 바꾸는 동작을
i = 0부터 i = (n - 2) 까지만 반복하고 끝낸다.
마지막 원소(인덱스 n-1)는 바꿀 대상이 자기 자신밖에 없으므로 포함하지 않는다.
장점
- 새로운 배열이 필요하지 않다.
소스 코드(C#)
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
private static System.Random random = new System.Random();
// Modern Fisher-Yates Shuffle
private void Shuffle<T>(T[] array)
{
int n = array.Length;
int last = n - 2;
for (int i = 0; i <= last; i++)
{
int r = random.Next(i, n); // [i, n - 1]
Swap(i, r);
}
// Local Method
void Swap(int idxA, int idxB)
{
T temp = array[idxA];
array[idxA] = array[idxB];
array[idxB] = temp;
}
}