내적
…
특징
- 내적은 벡터의 차원에 관계 없이, 동일한 차원의 벡터끼리 가능하다.
- 내적의 결과는 스칼라 값이다.
- 벡터
A,B의 내적은A를B에(또는B를A에) 투영시킨 후 두 벡터의 길이를 곱한 것과 같다. - 내적은 교환 법칙, 결합 법칙이 성립한다.
주어진 벡터
\[\begin{flalign*} \quad A = (a_{x} \, , \,\, a_{y} \, , \,\, a_{z}) && \end{flalign*}\] \[\begin{flalign*} \quad B = (b_{x} \, , \,\, b_{y} \, , \,\, b_{z}) && \end{flalign*}\]내적 연산
\[\begin{flalign*} \quad A \cdot B = a_{x} \cdot b_{x} + a_{y} \cdot b_{y} + a_{z} \cdot b_{z} && \end{flalign*}\] \[\begin{flalign*} \quad \,\, A \cdot B = |A| |B| cos\theta && \end{flalign*}\]내적의 활용
[1] 두 벡터의 각도 관계 판별하기
…
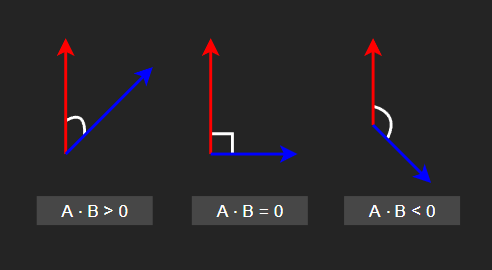
- 두 벡터의 내적 결과가 0보다 크면 두 벡터가 이루는 각도는 예각이다.
- 두 벡터의 내적 결과가 0이면 두 벡터가 이루는 각도는 직각이다.
- 두 벡터의 내적 결과가 0보다 작으면 두 벡터가 이루는 각도는 둔각이다.
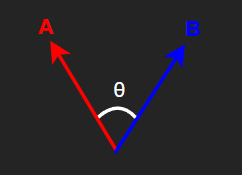
[2] 두 벡터의 사잇각 계산하기
…
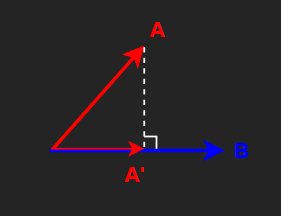
[3] 다른 벡터에 투영하기
…
[4] 평면에 투영하기
…
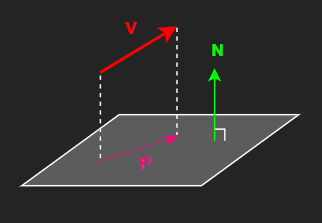
V : 벡터
N : 평면의 법선 벡터(크기 1)
V’ : 법선 벡터(N)에 투영된 V 벡터
P : 평면에 투영된 V 벡터
벡터 V를 법선 벡터 N에 투영한다.
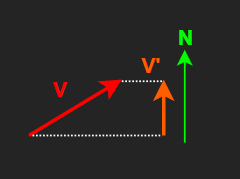
벡터 V에서 V'을 뺀다.
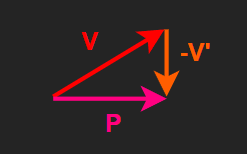
하나의 식으로 정리하면 다음과 같다.
\[\begin{flalign*} \qquad P = V - (V \cdot N) \, N && \end{flalign*}\]외적
…
특징
- 벡터의 외적은 3차원 벡터끼리만 가능하다.
- 외적의 결과는 벡터 값이다.
- 두 벡터를 외적한 결과는 두 벡터 모두에 수직인 벡터와 같다.
- 외적은 교환 법칙, 결합 법칙이 성립하지 않는다.
- 좌표계 종류(왼손, 오른손)에 따라 외적 결과 벡터의 방향이 달라진다.
주어진 벡터
\[\begin{flalign*} \quad A = (a_{x} \, , \,\, a_{y} \, , \,\, a_{z}) && \end{flalign*}\] \[\begin{flalign*} \quad B = (b_{x} \, , \,\, b_{y} \, , \,\, b_{z}) && \end{flalign*}\]외적 연산
\[\begin{flalign*} \quad A \times B = \begin{vmatrix} i & j & k \\ a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \end{vmatrix} \\ && \end{flalign*}\] \[\begin{flalign*} \qquad \qquad = i \begin{vmatrix} a_{y} & a_{z} \\ b_{y} & b_{z} \end{vmatrix} - j \begin{vmatrix} a_{x} & a_{z} \\ b_{x} & b_{z} \end{vmatrix} + k \begin{vmatrix} a_{x} & a_{y} \\ b_{x} & b_{y} \end{vmatrix} \\ && \end{flalign*}\] \[\begin{flalign*} \qquad \quad = (a_{y} \cdot b_{z} - a_{z} \cdot b_{y} \, , \, \, a_{z} \cdot b_{x} - a_{x} \cdot b_{z} \, , \, \, a_{y} \cdot b_{z} - a_{z} \cdot b_{y})&& \end{flalign*}\]외적의 활용
[1] 두 벡터에 수직인 벡터 계산하기
…
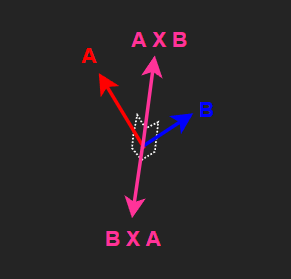
두 벡터의 외적 결과는 두 벡터 모두에 수직인 벡터이며,
순서를 바꾸어 연산할 경우 반대 방향으로 수직인 벡터를 얻을 수 있다.
\[\begin{flalign*} \quad A \times B = -B \times A && \end{flalign*}\][2] 외적 결과 벡터의 길이 구하기
…
두 벡터 A, B를 외적한 벡터의 길이는 다음과 같이 계산할 수 있다.
[3] 평면의 법선 벡터 구하기
…
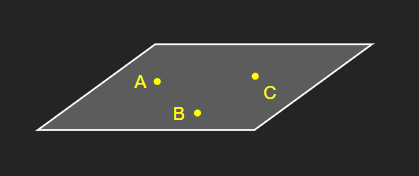
세 개의 점을 알고 있을 때,
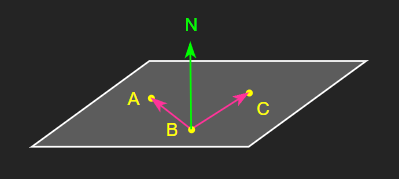
세 개의 점 중 두 개를 지나는 서로 다른 벡터를 외적하여 평면의 법선 벡터를 손쉽게 구할 수 있다.
[4] 벡터의 좌우 관계 판별하기
…
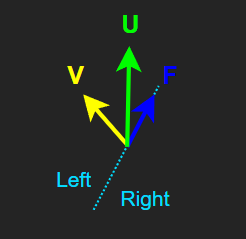
F : 전방(Forward) 벡터
U : 상단(Up) 벡터
V : 좌우 관계를 판별할 벡터
k > 0이면 벡터V는 좌측을 향한다.k = 0이면 벡터V는 중앙을 향한다. (F와U가 이루는 평면에 포함된다.)k < 0이면 벡터V는 우측을 향한다.
[5] 오브젝트의 로컬 축 벡터 구성하기
…
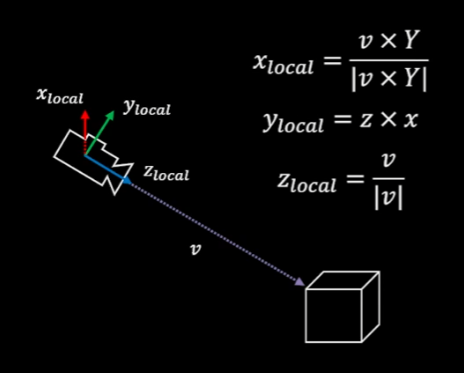
v : 정규화되지 않은 전방 벡터(주어진 벡터)
Y : 월드 Y 벡터(주어진 벡터)
local Z:v벡터 정규화local X: localZ × worldYlocal Y: localZ × localX
[6] 삼각형의 내부, 외부 판별하기
…
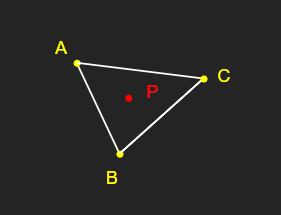
벡터 AB, BC, CA 중 두 개의 벡터를 외적하여
점 A, B, C가 이루는 평면의 법선 벡터 N을 구한다.
위의 [3] 방법을 통해 판별하여,
점 P가 벡터 AB, BC, CA에 대해 각각 모두 좌측에 위치한 경우
점 P는 삼각형 ABC의 내부에 있다고 판단할 수 있다.
Note
실제로 사용하기에는 성능이 매우 떨어지므로,
아핀 조합에 의한 방정식
\[\begin{flalign*} \quad P = aA + bB + (1 - a - b)C && \end{flalign*}\]에 대해
a, b, a + b가 모두 [0, 1] 범위 내에 있다면
점 P는 삼각형 내부에 있는 것으로 판정하는 방법을 사용한다.
추가
…
[1] 벡터 삼중곱
- 라그랑주 공식 또는 백캡 규칙(BAC-CAB rule) 이라고도 한다.
- 외적은 결합법칙이 성립하지 않으므로
A×(B×C)는(A×B)×C와 다르다.
[2] 스칼라 삼중곱
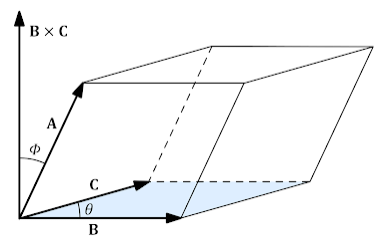
- 스칼라 삼중곱의 절댓값을 통해 위 평행 육면체의 부피를 구할 수 있다.