3D 게임 공간의 확장
- 벡터 공간 : 이동 벡터를 표현(w가 항상 0)
- 아핀 공간 : 위치 벡터를 표현(w가 항상 1)
특징
- 벡터와 벡터는 더할 수 있다.
- 벡터와 점을 더하면
w = 1이므로 점이 된다. - 점과 점을 더하면
w = 2가 되어 아핀 공간을 벗어나므로, 더할 수 없다.
아핀 조합(Affine Combination)
\[a + b = 1\] \[P = aP_{1} + bP_{2}\] \[P = aP_{1} + (1 - a)P_{2}\]
- 점
P는(x, y, z, 1)인 아핀 공간의 위치 벡터 - 아핀 조합 : 아핀 공간의 두 점을 더했을 때의 결과가 아핀 공간의 점(w = 1)이 됨을 보장하는 공식
두 개의 점을 이용해 선 표현하기
\(P = aP_{1} + (1 - a)P_{2}\)
-
a: 계수 (a = 1)이면 P는 P1(a = 0)이면 P는 P2
a가 실수이면 P는 직선(Line)
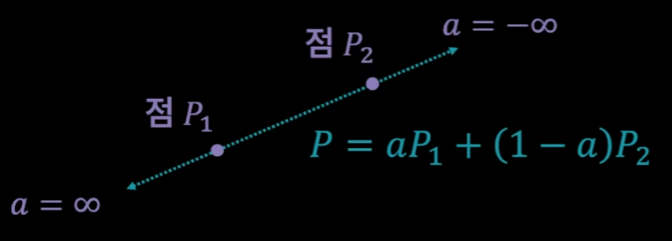
(a > 0)이면 P2에서 P1을 향한 반직선(Ray)

(0 < a < 1)이면 P1과 P2 사이의 선분(Line Segment)

세 개의 점을 이용해 평면 표현하기
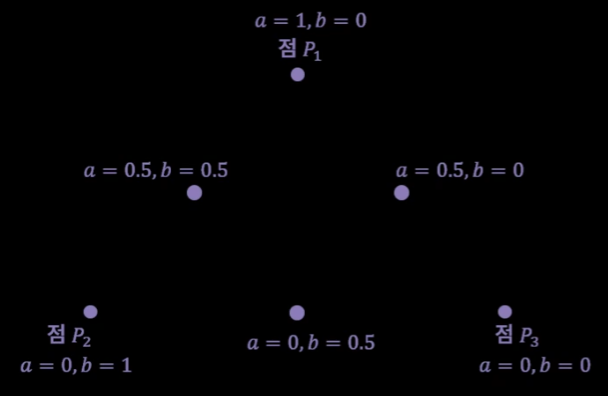
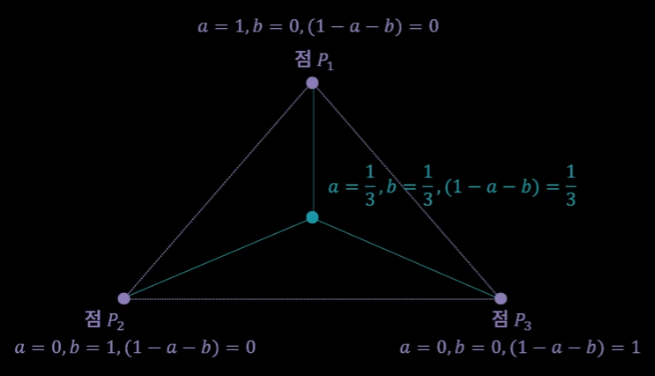
\(P = aP_{1} + bP_{2} + (1 - a - b)_{3}\)
a,b: 계수
- (
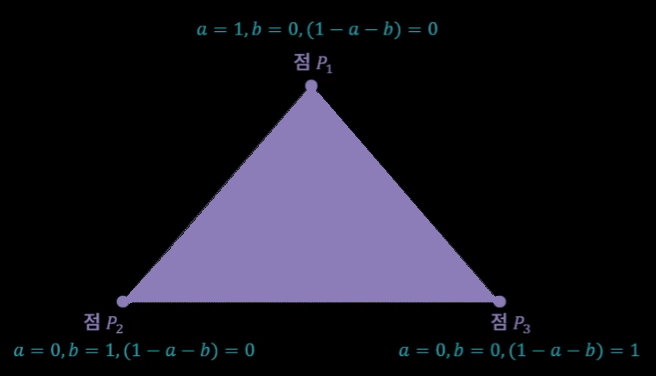
a = 1,b = 0,(1 - a - b) = 0)이면 P는 P1 - (
a = 0,b = 1,(1 - a - b) = 0)이면 P는 P2 -
(
a = 0,b = 0,(1 - a - b) = 1)이면 P는 P3 a,b가 실수이면 P는 점 P1, P2, P3를 모두 지나는 평면

- (
0 < a < 1,0 < b < 1,0 < a + b < 1)이면 P는 점 P1, P2, P3가 이루는 삼각형

- 모든 계수(
a,b,(1 - a - b))가1/3일 때 P는 무게중심좌표(Barycentric Coordinate)
정점 데이터의 보간
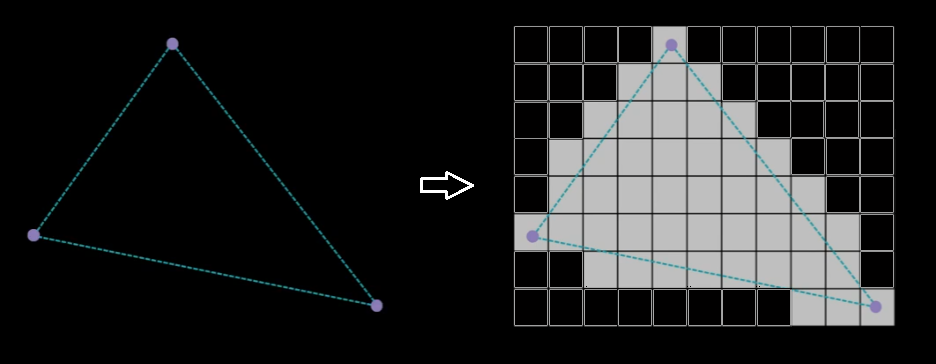
픽셀화(Rasterization)
- 세 개의 정점 데이터를 이용해 각 정점 사이의 픽셀 데이터를 계산하는 것
- 각 정점이 갖고 있던 데이터가 위의 평면 방정식을 통해 계수
(0 ~ 1)사이에서 보간되어 삼각형 내의 픽셀들에 적용된다.
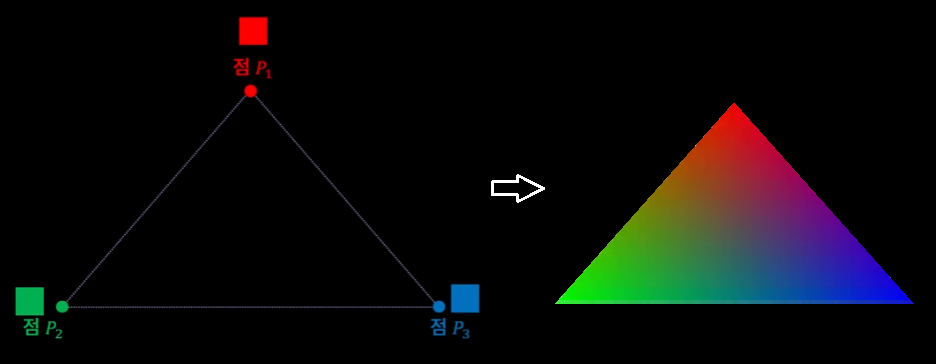
색상 보간 예시
- 세 개의 정점이 각각
R,G,B색상을 가지고 있었을 경우, 평면의 보간을 통해 삼각형의 내부를 아래와 같이 채울 수 있다.