트리 자료 구조
트리(Tree)
- 재귀적 계층 구조
- 노드로 이루어져 있다.
- 최초의 루트 노드에서부터 시작하며, 하나의 부모 노드는 여러 개의 자식 노드를 가진다.
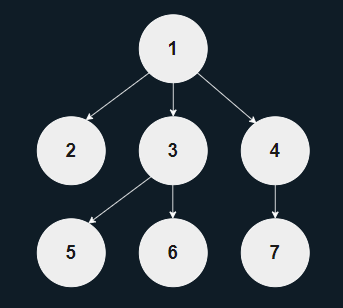
이진 트리(Binary Tree)
- 각 노드가 최대 두 개의 자식만 가질 수 있는 트리 구조
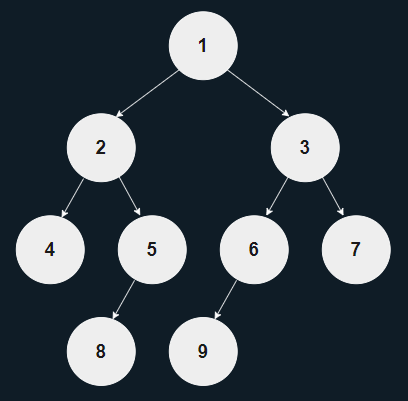
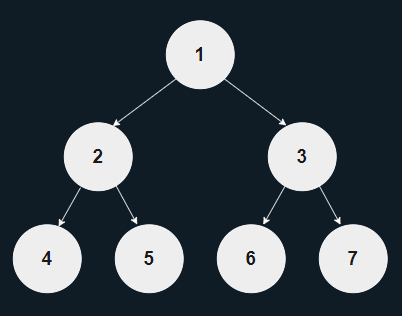
포화 이진 트리(Perfect Binary Tree)
- 모든 잎 노드(Leaf Node : 자식이 없는 노드)가 같은 계층에 위치한 노드
- 완전한 삼각형 꼴을 이룬 이진 트리 구조를 의미한다.
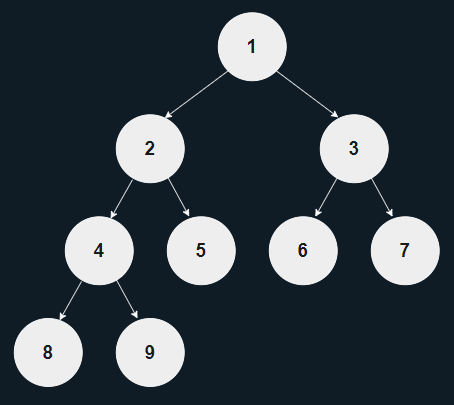
완전 이진 트리(Complete Binary Tree)
- 마지막 계층 이전까지의 계층이 포화 이진 트리를 이룬 구조
- 마지막 계층은 왼쪽에서부터 채워지는 구조
- 일차원 배열을 통해 표현될 수 있다.
힙(Heap)
-
완전 이진 트리의 일종
-
최소 힙(Min Heap), 최대 힙(Max Heap)이 있다.
-
일차원 배열을 통해 주로 구현된다.
최소 힙(Min Heap)
-
루트 노드에 언제나 트리 내의 최솟값이 위치한다.
-
부모 노드는 항상 자식 노드들보다 작은 값을 갖는다.
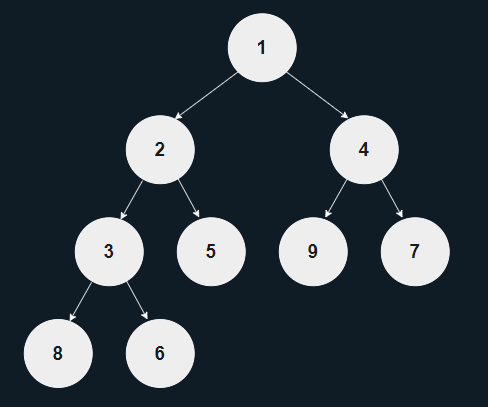
최대 힙(Max Heap)
-
루트 노드에 언제나 트리 내의 최댓값이 위치한다.
-
부모 노드는 항상 자식 노드들보다 큰 값을 갖는다.
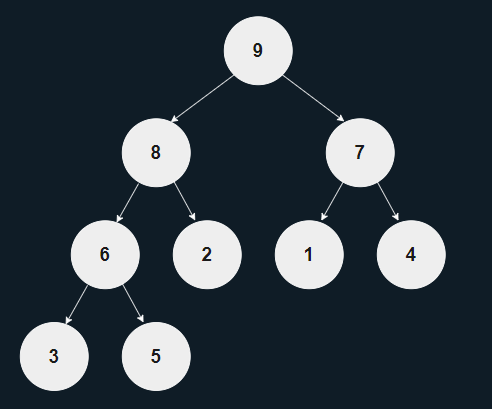
시간복잡도
- 힙의 삽입, 삭제 시간복잡도는
O(log(N))이다.
노드 삽입(예시 : 최소 힙)
삽입
- 새로운 노드를 힙의 마지막 위치에 삽입한다.
- 힙의 요건을 충족할 수 있도록, 새롭게 추가한 노드와 그 부모 노드를 비교하여 부모 노드보다 값이 작으면 서로 바꾼다.
- 힙의 요건이 충족될 때까지 부모 노드들을 거슬러 올라가며 반복한다.
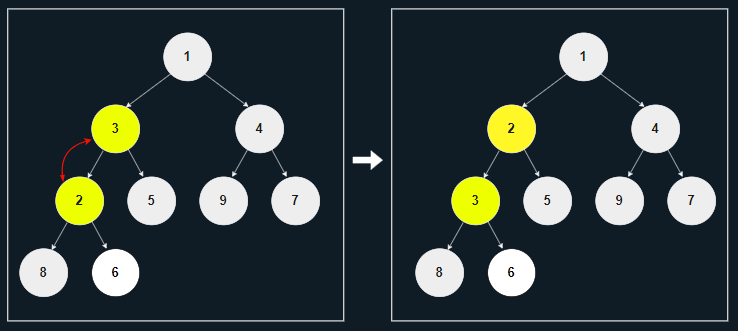
[1] 마지막 위치에 노드 2를 삽입한다.
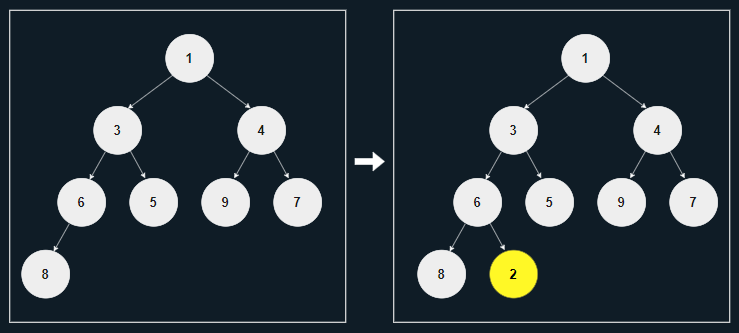
[2] 부모 노드의 값인 6이 2보다 작으므로 서로 바꾼다.
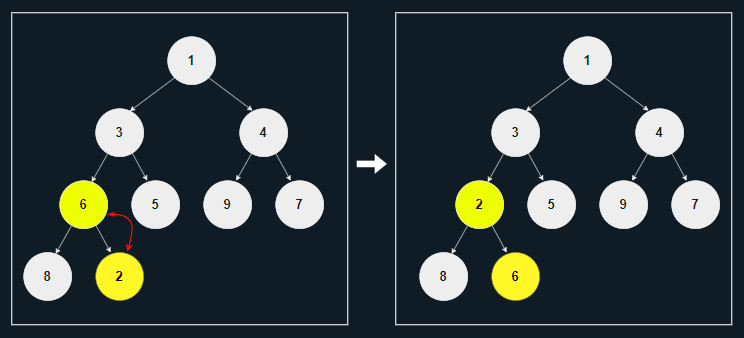
[3] 부모 노드의 값인 3이 2보다 작으므로 서로 바꾼다.
삽입 최적화
- 새로운 노드 삽입 이후 부모 노드와 비교하여 교환하는 동작은 (임시 변수에 A 할당 - A에 B 할당 - B에 임시 변수 할당)이라는 전통적인
Swap(A, B)연산을 사용해, 3번의 초기화를 통해 구현해야 한다. - 이를 최적화하여 미리 새로운 노드를 캐싱(저장)한 뒤 각 단계마다 부모를 자식 위치에 할당하기만 하고, 거슬러 올라가기를 멈춘 지점에 새로운 노드를 할당하는 방식으로 비용을 1/3 정도로 줄일 수 있다.
- 매 수행마다 캐싱된 노드가 위치할 인덱스를 저장하면서 진행하여, 진행을 멈췄을 때의 위치에 새로운 노드를 넣으면 된다.
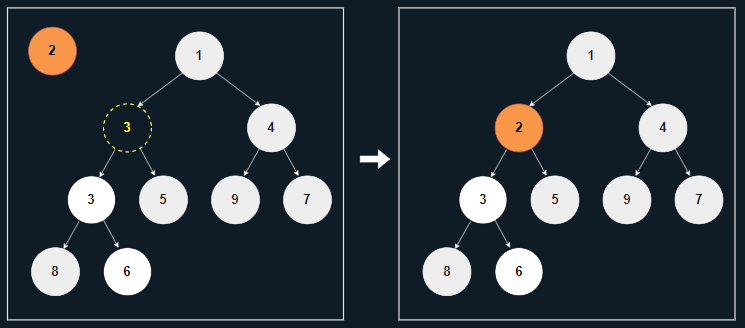
[1] 새로운 노드 2를 삽입할 위치(마지막 위치)를 확보하고, 노드를 일단 따로 저장한다.
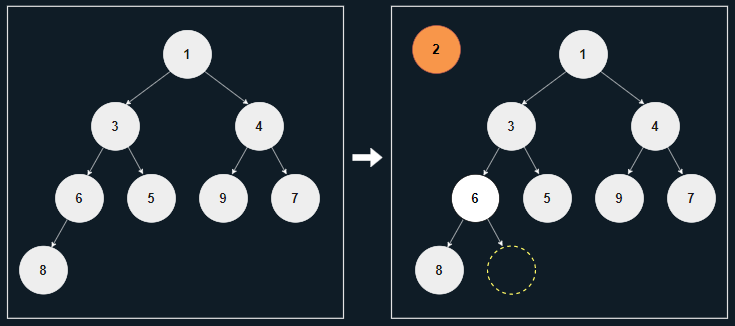
[2] 새로운 노드 2보다 6이 크므로, 노드 6을 마지막 위치로 옮긴다.
- 노드 6이 복제되며 원래 있던 자리에도 그대로 남아 있더라도, 일단 내버려 둔다.
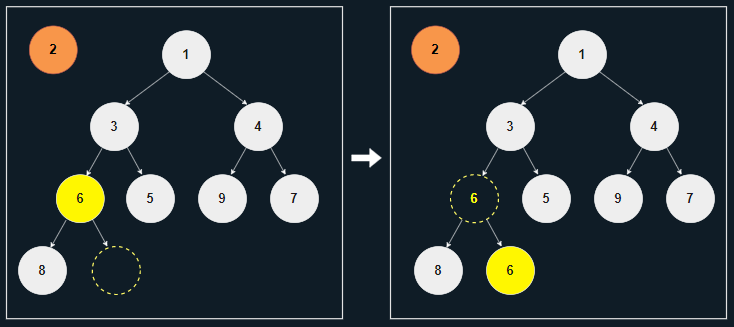
[3] 새로운 노드 2보다 3이 크므로, 노드 6이 원래 있던 위치에 노드 3을 옮긴다.
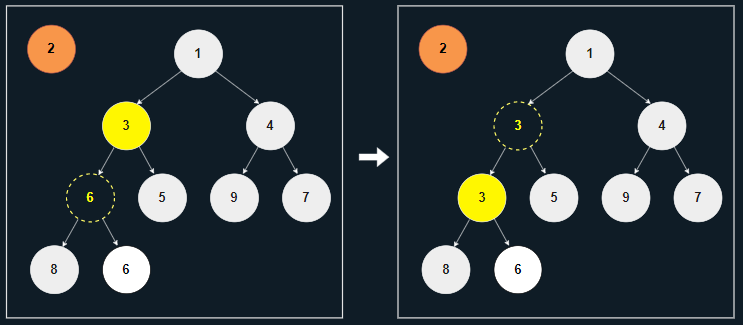
[4] 힙의 조건이 모두 충족되었으므로, 노드 3이 있던 위치에 노드 2를 삽입한다.
노드 삭제(예시 : 최소 힙)
삭제
- 기존의 노드를 삭제하고, 마지막 노드를 그 위치로 옮긴다.
- 옮긴 노드와 그 위치의 두 자식 노드를 비교하여, 가장 작은 자식보다 자신이 큰 경우 서로 바꾼다.
- 힙이 성립할 때까지 자식들과 비교하여 이를 반복한다.
[1] 노드 1을 삭제하고 마지막 노드인 6을 그 위치로 옮긴다.
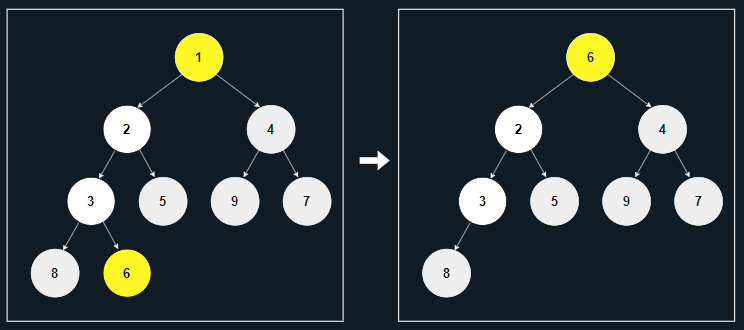
[2] 두 자식 중 가장 작은 자식인 2보다 6이 크므로, 서로 바꾼다.
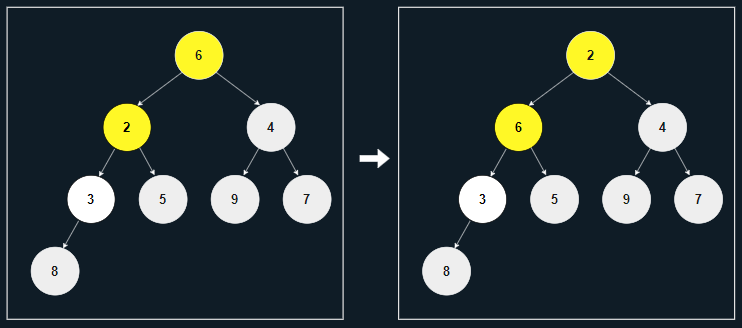
[3] 다음 위치에서 가장 작은 자식인 3보다 6이 더 크므로, 서로 바꾼다.
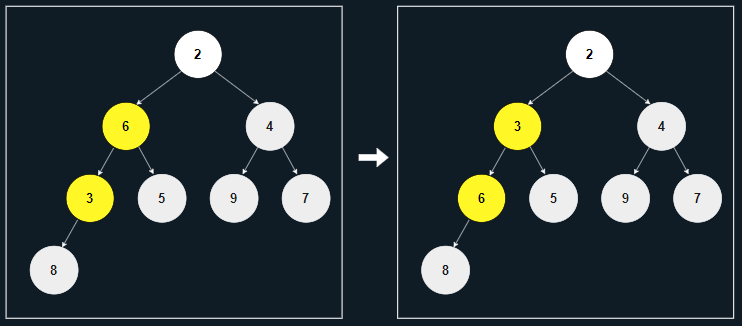
삭제 최적화
- 삽입의 최적화와 동일한 방식을 사용한다.
- 미리 마지막 노드를 제거하여 캐싱(저장)해두고, 제거한 노드의 위치에서부터 캐싱된 노드와 해당 위치의 자식 노드들을 비교한다.
- 진행 중인 현재 위치에서 더 작은 자식 노드보다 캐싱된 노드의 값이 클 경우, 서로를 바꾸는 대신에 그냥 자식 노드만 부모 위치로 올린 뒤 해당 자식 위치에서 다음 비교을 이어나간다.
- 매 수행마다 캐싱된 노드가 위치할 인덱스를 저장하면서 진행하여, 진행을 멈췄을 때의 위치에 새로운 노드를 넣으면 된다.
[1] 마지막 노드 6을 제거하고, 따로 저장한다.
- 제거될 노드 1은 삭제 연산의 반환 값이 필요하면 미리 따로 저장하고, 필요 없다면 그냥 둔다.
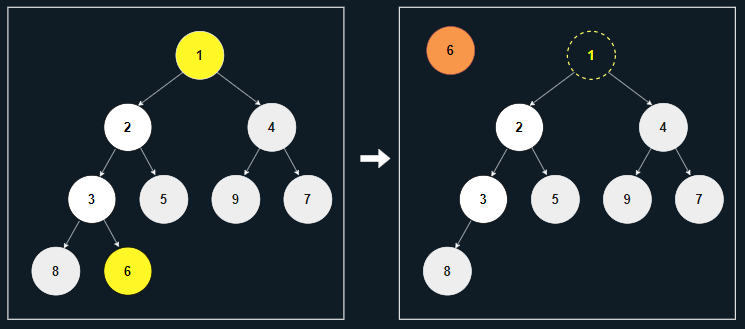
[2] 두 자식 노드 중 가장 작은 2가 6보다 작으므로, 노드 2를 부모 위치로 옮긴다.
- 노드 2가 복제되며 원래 위치에도 남아 있을 수 있으나, 상관 없으니 그냥 둔다.
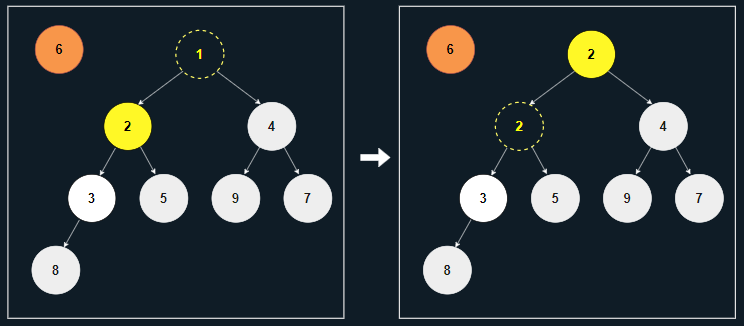
[3] 다음 두 자식 노드 중 가장 작은 3이 6보다 작으므로, 노드 3을 부모 위치로 옮긴다.
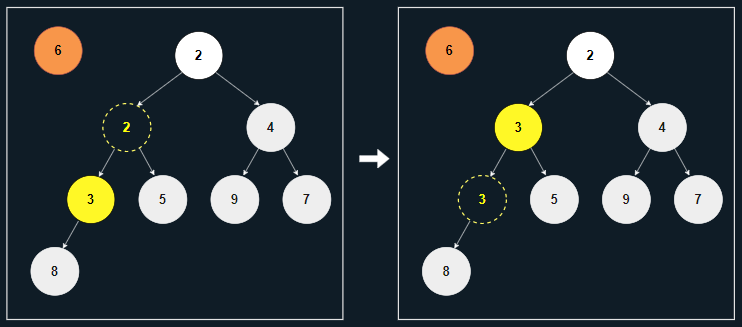
[4] 힙의 조건이 모두 충족되었으므로, 멈춘 위치에 노드 6을 삽입한다.
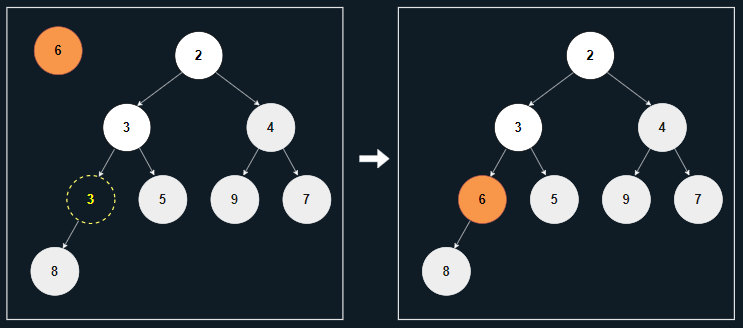
힙 정렬(Heap Sort)
힙의 루트를 제거하기를 반복하면서, 제거된 노드를 새로운 배열에 인덱스 0부터 차례대로 저장하기만 하면 최소 힙(Min Heap)일 경우 오름차순, 최대 힙(Max Heap)일 경우 내림차순으로 정렬되는 것이나 다름없다.
따라서 힙의 삽입을 모두 수행한 뒤, 힙이 빌 때까지 루트 노드의 삭제 연산을 모두 수행하면 그것이 힙 정렬이다.
배열을 이용해 힙 구현하기
- 힙은 완전 이진 트리 구조이므로, 배열을 통해 구현할 수 있다.
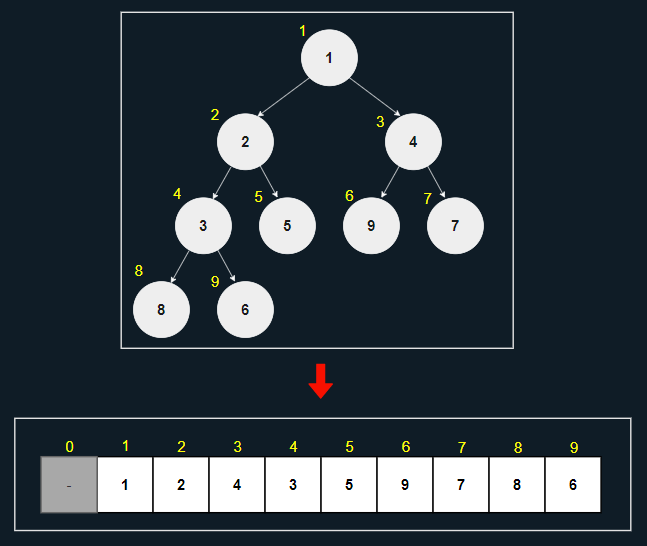
배열 인덱스 1에 루트 노드가 위치할 경우
- 왼쪽 자식 노드의 배열 내 인덱스는
(부모 노드의 인덱스 * 2)이다. - 오른쪽 자식 노드의 배열 내 인덱스는
(부모 노드의 인덱스 * 2 + 1)이다. - 부모 노드의 배열 내 인덱스는
(자식 노드의 인덱스 / 2)이다.
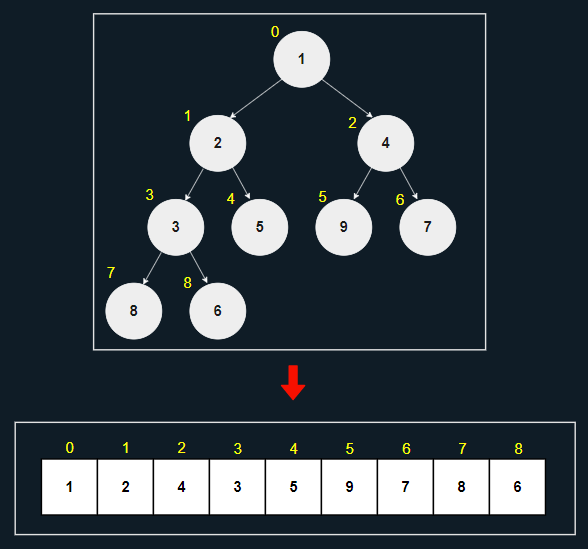
배열 인덱스 0에 루트 노드가 위치할 경우
- 왼쪽 자식 노드의 배열 내 인덱스는
(부모 노드의 인덱스 * 2 + 1)이다. - 오른쪽 자식 노드의 배열 내 인덱스는
(부모 노드의 인덱스 * 2 + 2)이다. - 부모 노드의 배열 내 인덱스는
((자식 노드의 인덱스 - 1) / 2)이다.
Min Heap 구현(C언어)
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
#include <stdio.h>
#define TRUE 1
#define MAX_SIZE 100
int heap[MAX_SIZE];
int heapSize = 0;
// 새로운 값을 넣고 힙 재구축
void Push(int item)
{
// 힙 크기 하나 증가, 순회 시작 인덱스(마지막 노드) 초기화
int i = heapSize++;
// 마지막 인덱스로부터 부모로 이동하며
// 자식이 부모보다 작으면 부모에 자식 초기화
while (i > 0 && item < heap[(i - 1) / 2])
{
int idxParent = (i - 1) / 2;
heap[i] = heap[idxParent];
i = idxParent;
}
// 인덱스가 멈춘 위치에 새로운 값 넣기
heap[i] = item;
}
// 힙의 루트를 꺼내어 리턴하고 힙 재구축
int Pop()
{
heapSize--; // 개수 하나 제거
int ret = heap[0]; // 최솟값(루트) 캐싱
int valLast = heap[heapSize]; // 마지막 노드 캐싱
// 루트에서부터 더 작은 자식을 부모로 옮기기
int i = 0; // current
while(TRUE)
{
int idxNC; // Index of Next Child
int idxLC = i * 2 + 1; // Index of Left Child
int idxRC = idxLC + 1; // Index of Right Child
// 좌측 자식이 범위를 벗어난 경우, 종료
if(idxLC > heapSize)
break;
// 우측 자식이 범위를 벗어난 경우, 다음 자식으로 좌측 선택
if(idxRC > heapSize)
{
idxNC = idxLC;
}
// 두 자식 모두 범위 내에 있는 경우, 더 작은 자식 선택
else
{
idxNC = (heap[idxLC] < heap[idxRC]) ? idxLC : idxRC;
}
// 자식이 부모보다 작은 경우, 부모로 옮기고 다음 순회 준비
if(heap[idxNC] < valLast)
{
heap[i] = heap[idxNC];
i = idxNC;
}
// 자식이 부모보다 큰 경우 순회 종료
else
break;
}
// 캐싱해뒀던 값을 순회 멈춘 자리에 초기화
heap[i] = valLast;
return ret;
}
void Print()
{
printf("Print Heap : ");
for (int i = 0; i < heapSize; i++)
{
printf("%d ", heap[i]);
}
printf("\n");
}
int main(void)
{
int last = 9;
for(int i = last; i >= 0; i--)
{
Push(i); Print();
}
for(int i = 0; i < last; i++)
{
Pop(); Print();
}
}
Heap 구현(C#)
- Min Heap, Max Heap 선택 가능한 클래스 구현
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
using System;
class Heap<T> where T : IComparable<T>
{
private T[] _array;
private int _size;
private readonly bool _isMinHeap;
public int Count => _size;
public bool IsEmpty => _size == 0;
public Heap(int capacity = 8, bool isMinHeap = true)
{
if (capacity < 4)
capacity = 4;
_array = new T[capacity];
_size = 0;
_isMinHeap = isMinHeap;
}
public Heap(bool isMinHeap, int capacity = 8) : this(capacity, isMinHeap) { }
/// <summary> 배열을 두 배로 확장 </summary>
private void ExpandArray()
{
T[] newArray = new T[_array.Length * 2];
Array.Copy(_array, newArray, _size);
_array = newArray;
}
/// <summary> 비교 연산 </summary>
private bool Compare(in T a, in T b)
{
return _isMinHeap ?
a.CompareTo(b) > 0 :
a.CompareTo(b) < 0;
}
/// <summary> 새로운 값 추가하기 </summary>
public void Push(T item)
{
// 배열이 가득 찬 경우, 확장
if (_array.Length == _size)
{
ExpandArray();
}
// 시작 인덱스 : 마지막 노드
int idx = _size++;
// 마지막 노드에서부터 차례로 부모 탐색
while (idx > 0) // 루트에 도달하면 종료
{
int idxParent = (idx - 1) / 2;
// 힙의 조건을 만족하게 된 경우, 중지
if (Compare(item, _array[idxParent]))
break;
// 자식 노드에 부모 값 넣은 뒤 부모로 이동
_array[idx] = _array[idxParent];
idx = idxParent;
}
// 탐색 멈춘 위치에 새로운 값 할당
_array[idx] = item;
}
/// <summary> 루트 노드의 값 제거 및 반환 </summary>
public T Pop()
{
if (IsEmpty)
return default;
// 루트 값 캐싱
T root = _array[0];
// 마지막 노드 값 캐싱 및 크기 하나 감소
T last = _array[--_size];
int idx = 0;
while (true)
{
int idxLC = idx * 2 + 1;
int idxRC = idxLC + 1;
int idxNext;
// 왼쪽 자식이 범위를 벗어난 경우 종료
if (idxLC >= _size)
break;
// 오른쪽 자식이 범위를 벗어난 경우, 왼쪽 자식 선택
if (idxRC >= _size)
{
idxNext = idxLC;
}
// 두 자식 모두 범위 내인 경우, 알맞게 선택
else
{
idxNext = Compare(_array[idxLC], _array[idxRC]) ? idxRC : idxLC;
}
// 힙 조건을 모두 충족하게 된 경우, 순회 종료
if (Compare(_array[idxNext], last))
break;
// 부모에 선택된 자식 값 초기화
_array[idx] = _array[idxNext];
// 인덱스를 선택된 자식으로 이동
idx = idxNext;
}
// 순회 멈춘 위치에 마지막 노드 값 초기화
_array[idx] = last;
return root;
}
/// <summary> 루트 노드 값 참조 </summary>
public T Peek()
{
if (IsEmpty)
return default;
return _array[0];
}
}
우선순위 큐(Priority Queue)
개념
-
이름에 큐(Queue)가 들어가지만, 큐와는 다르다.
-
우선순위를 갖는 요소를 삽입/삭제한다.
-
우선순위 큐에서 요소를 꺼내면 우선순위 순서대로 꺼내진다.
-
간단히 말해, Min Heap 또는 Max Heap이다.
-
링크드리스트(Linked List), 힙 등을 통해 구현할 수 있으며, 힙으로 구현하는 것이 효율적이다.
소스코드(C#)
- 그냥 Min Heap이다.
…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
using System;
class PriorityQueue<T> where T : IComparable<T>
{
private T[] _array;
private int _size;
public int Count => _size;
public bool IsEmpty => _size == 0;
public PriorityQueue(int capacity = 8)
{
if (capacity < 4)
capacity = 4;
_array = new T[capacity];
_size = 0;
}
/// <summary> 배열을 두 배로 확장 </summary>
private void ExpandArray()
{
T[] newArray = new T[_array.Length * 2];
Array.Copy(_array, newArray, _size);
_array = newArray;
}
/// <summary> 비교 연산 </summary>
private bool Compare(in T a, in T b)
{
return a.CompareTo(b) > 0;
}
/// <summary> 새로운 값 추가하기 </summary>
public void Push(T item)
{
// 배열이 가득 찬 경우, 확장
if (_array.Length == _size)
{
ExpandArray();
}
// 시작 인덱스 : 마지막 노드
int idx = _size++;
// 마지막 노드에서부터 차례로 부모 탐색
while (idx > 0) // 루트에 도달하면 종료
{
int idxParent = (idx - 1) / 2;
// 힙의 조건을 만족하게 된 경우, 중지
if (Compare(item, _array[idxParent]))
break;
// 자식 노드에 부모 값 넣은 뒤 부모로 이동
_array[idx] = _array[idxParent];
idx = idxParent;
}
// 탐색 멈춘 위치에 새로운 값 할당
_array[idx] = item;
}
/// <summary> 루트 노드의 값 제거 및 반환 </summary>
public T Pop()
{
if (IsEmpty)
return default;
// 루트 값 캐싱
T root = _array[0];
// 마지막 노드 값 캐싱 및 크기 하나 감소
T last = _array[--_size];
int idx = 0;
while (true)
{
int idxLC = idx * 2 + 1;
int idxRC = idxLC + 1;
int idxNext;
// 왼쪽 자식이 범위를 벗어난 경우 종료
if (idxLC >= _size)
break;
// 오른쪽 자식이 범위를 벗어난 경우, 왼쪽 자식 선택
if (idxRC >= _size)
{
idxNext = idxLC;
}
// 두 자식 모두 범위 내인 경우, 알맞게 선택
else
{
idxNext = Compare(_array[idxLC], _array[idxRC]) ? idxRC : idxLC;
}
// 힙 조건을 모두 충족하게 된 경우, 순회 종료
if (Compare(_array[idxNext], last))
break;
// 부모에 선택된 자식 값 초기화
_array[idx] = _array[idxNext];
// 인덱스를 선택된 자식으로 이동
idx = idxNext;
}
// 순회 멈춘 위치에 마지막 노드 값 초기화
_array[idx] = last;
return root;
}
/// <summary> 루트 노드 값 참조 </summary>
public T Peek()
{
if (IsEmpty)
return default;
return _array[0];
}
}