레이 마칭이란?
-
메시 데이터를 이용하는 기존의 3D 렌더링 방식과는 달리, 거리 함수(SDF)를 통해 오브젝트의 표면을 정의한다.
-
카메라로부터 스크린 픽셀들을 향해 레이를 전진시키고(Ray Marching), 해당 픽셀의 레이가 오브젝트 표면에 닿으면 그 픽셀에 오브젝트 표면을 렌더링하는 방식을 사용한다.

SDF
- Signed Distance Function
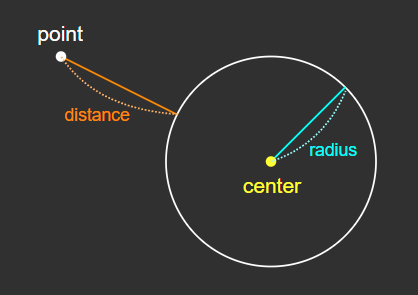
- 공간 상의 임의의 한 점으로부터 오브젝트 표면까지의 최단 거리를 계산하는 함수
- SDF를 통해 3D 오브젝트 표면의 공간상 위치를 정의할 수 있다.
- 가장 간단한 SDF : 구체(Sphere)
1
2
3
4
5
6
7
// point : 거리를 계산할 기준 좌표
// center : Sphere의 중심 좌표
// radius : Sphere의 반지름
float sdSphere(vec3 point, vec3 center, float radius)
{
return length(point - center) - radius;
}
레이 마칭 과정
[1] Ray Origin 정의

레이의 출발 지점(Ray Origin, RO), 즉 카메라의 3D 공간 상 위치를 정의한다.
[2] Screen UV 정의

XY 평면에 Screen UV(화면 좌표)를 정의한다.
[3] Ray Direction 정의
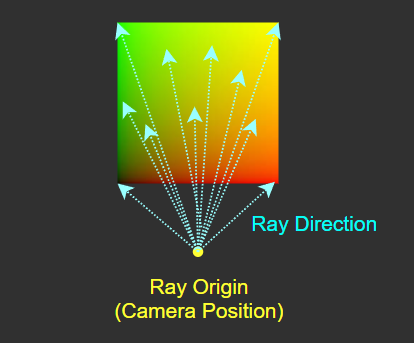
Screen UV 좌표에 깊이(Z축 좌표)를 추가하여 3D 공간 상의 화면 좌표를 생성한다.
그리고 카메라(RO)에서 모든 화면 좌표를 향하는 방향 벡터(Ray Direction, RD)를 정의한다.
RD는 정규화된 벡터여야 한다.
Note
레이 마칭은 대개 Pixel Shader 또는 Fragment Shader에서 계산한다.
물체의 표면을 이루는 모든 픽셀마다 한 번씩 병렬적으로 실행된다는 뜻이다.
다시 말해, RD는 각 픽셀 쉐이더마다 한 개씩 계산된다.
따라서 물체의 표면을 이루는 픽셀이 200 x 100 = 20000개라면 20000 개의 RD가 존재하고,
렌더 타겟, 즉 스크린 전체에서 레이 마칭을 계산하게 될 경우 해상도 만큼의 RD가 존재한다.
[4] SDF 정의
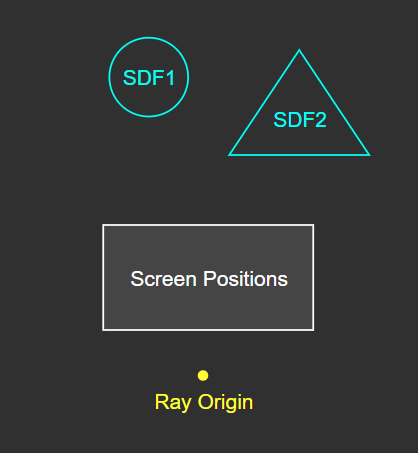
공간 상의 물체 표면 정보를 SDF 함수를 통해 정의한다.
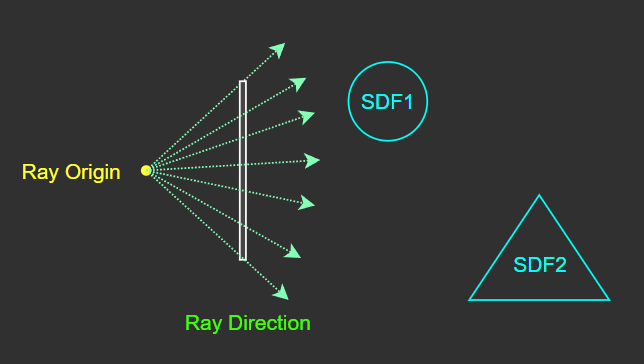
[5] 레이 전진 알고리즘
하나의 픽셀 쉐이더, 즉 하나의 RD에 대해 예시로 설명한다.
RO, RD, SDF가 모두 정의된 상태.

RO에서 각각의 물체마다 SDF(거리 함수)를 계산하여, RO로부터 각 물체 표면까지의 최단거리를 계산한다.
예시의 오브젝트는 2개이므로, 총 2개의 SDF 계산을 거쳐 두 개의 거리 값이 계산된다.
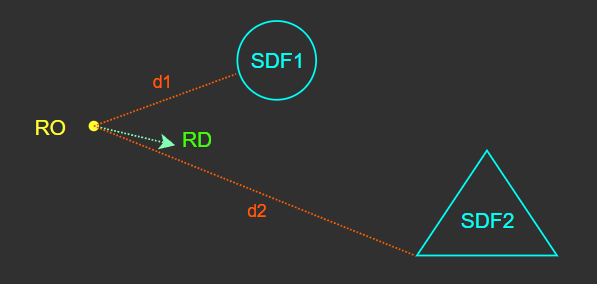
계산된 모든 SDF 값(d1, d2)들 중 가장 작은 값(d1)만큼의 거리를 RD 방향으로 전진한다.
그러면 한 번의 스텝(Step)이 완료된 것이다.
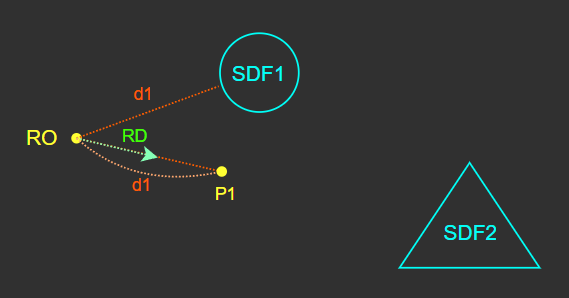
첫 번째 스텝에서 전진한 위치(P1)에서 다시 모든 물체의 SDF를 계산하여 각 물체 표면까지의 최단거리를 계산한다.

그리고 마찬가지로 각 최단거리 중 가장 작은 값만큼 RD 방향으로 전진한다.
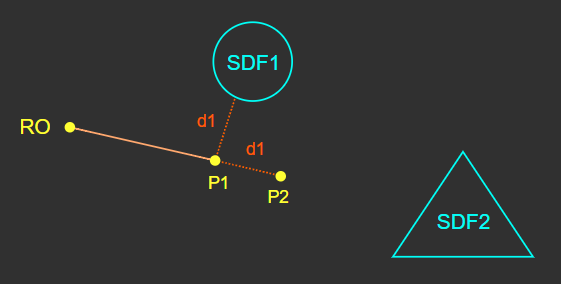
위와 같이 스텝을 반복하여 레이를 전진시키고, 이동한 거리 값을 누적한다.
물체 표면에 닿거나(최단거리가 임계 값보다 작다고 판단)
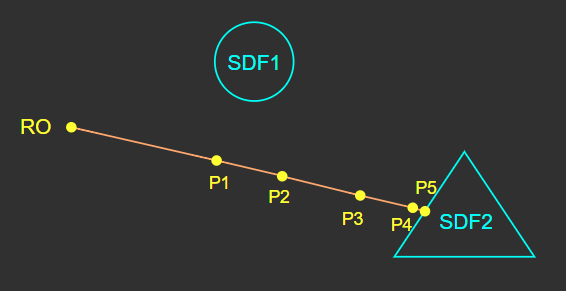
물체 표면을 찾지 못한 상태에서 제한 스텝 수 또는 제한 전진 거리에 도달한 경우
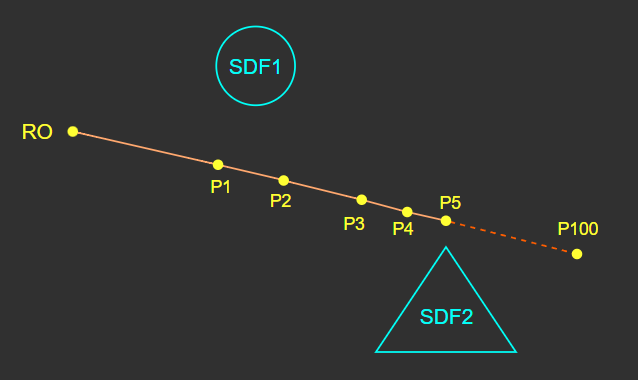
스텝을 종료한다.
레이마칭의 결과로는 RO에서부터 물체 표면까지의 거리(d)를 리턴하게 되는데,
RO + RD * d 계산식을 통해 물체 표면의 공간 상 위치를 계산할 수 있다.
레이 마칭 함수
레이 마칭 함수의 구성

출처 : Youtube - The Art of Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#define MAX_STEPS 100 // 최대 스텝 수
#define MAX_DIST 100 // 최대 전진 거리
#define SURF_DIST 0.01 // 표면 인식 거리
float RayMarch(vec3 ro, vec3 rd)
{
// RO에서 현재까지 전진한 누적 거리 저장
float dO = 0.;
for(int i = 0; i < MAX_STEPS; i++)
{
vec3 p = ro + rd * dO;
// GetDist() : 지정한 위치로부터 최단 SDF 거리값 계산
float dS = GetDist(p); // 이번 스텝에 전진할 거리
dO += dS; // 레이 전진
// 레이 제한 거리까지 도달하거나
// 레이가 물체의 정점 또는 땅에 닿은 경우 레이 마칭 종료
if(dO > MAX_DIST || dS < SURF_DIST)
break;
}
return dO;
}
- i : 누적 스텝 수
- ro : 카메라의 위치
- rd : 레이의 전진 방향(카메라 -> 스크린의 모든 픽셀)
- dO : 현재 스텝까지 레이의 누적 전진 거리
- dS : 이번 스텝에서 전진할 거리(즉, 모든 SDF를 계산했을 때 가장 작은 값)
- p : 레이의 현재 위치
- MAX_STEPS : 최대 반복(스텝) 횟수
- SURFACE_DIST : 레이가 표면에 닿았다고 판단할 임계값
- MAX_DIST : 레이가 전진할 수 있는 최대 거리
전체 계산 과정
[1] 거리 계산
- 스크린의 모든 픽셀에 대해 위의 레이마칭 과정을 통해 최단 거리 값을 계산한다.

RayMarch Function
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
float RayMarch(vec3 ro, vec3 rd)
{
// RO에서 현재까지 전진한 누적 거리 저장
float dO = 0.;
for(int i = 0; i < MAX_STEPS; i++)
{
vec3 p = ro + rd * dO;
// GetDist() : 지정한 위치로부터 최단 SDF 거리값 계산
float dS = GetDist(p); // 이번 스텝에 전진할 거리
dO += dS; // 레이 전진
// 레이 제한 거리까지 도달하거나
// 레이가 물체의 정점 또는 땅에 닿은 경우 레이 마칭 종료
if(dO > MAX_DIST || dS < SURF_DIST)
break;
}
return dO;
}
[2] 노멀 계산
-
[1]에서 얻어낸 거리값(d)을 이용해, 각 표면의 정확한 3D 공간 상 위치(P = RO + RD * d)를 계산한다. -
계산된 위치(
P)로부터 x, y, z축 방향으로 각각 미세하게 떨어진 위치에서GetDist()함수를 통해 가장 가까운 물체 표면까지의 거리를 계산한다. -
이렇게 얻어낸 3개의 값을 각각 해당 표면에서의 x, y, z 노멀 벡터 성분으로 사용한다.

GetNormal Function
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 각 물체 표면 위치에서 노멀 벡터 계산
vec3 GetNormal(vec3 p)
{
float d = GetDist(p);
vec2 e = vec2(0.001, 0.0);
// x, y, z 좌표를 0.01씩 움직인 3개의 방향벡터를 이용하여
// 각각 GetDist()를 통해 해당 방향에 있는 물체의 표면까지의 최단거리를 찾고,
// 이를 x, y, z 성분으로 사용한 노멀 벡터 생성
vec3 n = d - vec3(
GetDist(p - e.xyy),
GetDist(p - e.yxy),
GetDist(p - e.yyx)
);
return normalize(n);
}
[3] 라이트(Directional Light) 계산
- 픽셀 쉐이더에서의 디퓨즈 계산 방식과 동일하게, 가상 라이트 벡터(L)와 각 표면의 노멀 벡터(N)를 내적하여 라이팅을 계산한다.

GetLight Function
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 각 물체 표면에서 라이팅 계산
float GetLight(vec3 p)
{
vec3 L = normalize(g_lightPos - p);
vec3 N = GetNormal(p);
// Shade(Diffuse)
float diff = saturate( dot(N, L) );
// Shadow
// 물체 표면에서 광원을 향해 레이마칭하여 얻은 거리가
// 표면에서 광원까지의 거리보다 작다면,
// 그 사이에 또다른 물체의 표면이 가로막고 있다는 뜻이므로 이 표면에는 그림자가 생긴다.
// SURF_DIST만큼의 거리를 더해주는 이유 : 레이가 정점을 찾아내는 최소 거리(Threshold)이므로
// SURF_DIST에 1.0 초과 숫자를 곱해주는 이유 : 의도치 않은 음영이 생길 수 있으므로
float d = RayMarch(p + N * SURF_DIST * 2.0, L);
if( d < length(g_lightPos - p) )
diff *= 0.1;
return diff;
}
ShaderToy에서의 구현 예시

Source Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
#define MAX_STEPS 100
#define MAX_DIST 100.0
#define SURF_DIST 0.01
// 광원
vec3 g_lightPos = vec3(0., 5., 1.);
/**************************************************************************************************
* 3D Objects
* https://iquilezles.org/www/articles/distfunctions/distfunctions.htm
* https://www.youtube.com/watch?v=Ff0jJyyiVyw
**************************************************************************************************/
struct Plane
{
vec3 normal; // 평면 법선 벡터의 방향
float height; // 높이 : 원점에서 normal벡터 방향으로 더한 값
};
struct Sphere
{
vec3 pos;
float radius;
};
struct Box
{
vec3 pos;
vec3 size;
};
// 속이 빈 박스
struct BoundingBox
{
vec3 pos;
vec3 size;
float e; // edge Thickness
};
// 도넛형
struct Torus
{
vec3 pos;
vec2 radius; // (out radius, in radius)
};
/**************************************************************************************************
* 3D Object Distance Functions
**************************************************************************************************/
// GetMinDist : 지점 p로부터 오브젝트 o위의 정점으로의 거리 중 가장 가까운 거리 찾아 리턴
float SD(vec3 p, Sphere o)
{
return length(p - o.pos) - o.radius;
}
float SD(vec3 p, Plane o)
{
return dot(p, normalize(o.normal)) - o.height;
}
float SD(vec3 p, Box o)
{
vec3 q = abs(p - o.pos) - o.size;
return length(max(q, 0.0)) + min( max(q.x, max(q.y,q.z) ), 0.0);
}
float SD(vec3 p, BoundingBox o)
{
vec3 b = o.size;
float e = o.e;
p = abs(p - o.pos )-b;
vec3 q = abs(p+e)-e;
return min(min(
length(max(vec3(p.x,q.y,q.z),0.0))+min(max(p.x,max(q.y,q.z)),0.0),
length(max(vec3(q.x,p.y,q.z),0.0))+min(max(q.x,max(p.y,q.z)),0.0)),
length(max(vec3(q.x,q.y,p.z),0.0))+min(max(q.x,max(q.y,p.z)),0.0));
}
float SD(vec3 p, Torus o)
{
p = p - o.pos;
vec2 r = o.radius;
vec2 q = vec2(length(p.xz)-r.x,p.y);
return length(q)-r.y;
}
/**************************************************************************************************
* Ray Marching Functions
**************************************************************************************************/
// 현재 진행중인 레이 위의 점에서 다음 지점(특정 오브젝트 표면 또는 플레인) 발견하여 리턴
// 현재 위치 p에서 구형범위로 탐색하여, 어떤 물체든 찾아 가장 작은 구체의 반지름을 리턴하는 것과 같음
float GetDist(vec3 p)
{
Plane pl;
pl.normal = vec3(0.0, 1.0, 0.0);
pl.height = 0.0;
Sphere s;
s.pos = vec3(-6.0, 1.0, 6.0);
s.radius = 1.0;
Box b;
b.pos = vec3(-2.0, 1.0, 6.0);
b.size = vec3(1.0, 1.0, 1.0);
BoundingBox bb;
bb.pos = vec3(1.0, 1.0, 6.0);
bb.size = vec3(1.0, 1.0, 1.0);
bb.e = 0.1;
Torus t;
t.pos = vec3(5.0, 1.0, 6.0);
t.radius = vec2(1.0, 0.4);
float dPlane = SD(p, pl); //p.y;
float dSphere = SD(p, s);
float dBox = SD(p, b);
float dBBox = SD(p, bb);
float dTorus = SD(p, t);
// 발견한 다음 지점들 중 가장 가까운 지점 리턴
float d = min(dPlane, dSphere);
d = min(d, dBox);
d = min(d, dBBox);
d = min(d, dTorus);
return d;
}
// ro(카메라)로부터 rd 방향(모든 uv 픽셀)으로 레이 발사
// 리턴값 : 카메라로부터 레이 방향에서 찾은 가장 가까운 정점
float RayMarch(vec3 ro, vec3 rd)
{
// RayMarch Distance From Origin : Ray Origin(카메라)에서부터의 거리
float dO = 0.;
for(int i = 0; i < MAX_STEPS; i++)
{
vec3 p = ro + rd * dO;
float dS = GetDist(p); // Distance to the Scene : 레이 내에서 다음 스텝으로 전진시킬 거리
dO += dS; // 레이 한 스텝 전진
// 레이 제한 거리까지 도달하거나
// 레이가 물체의 정점 또는 땅에 닿은 경우 레이 마칭 종료
if(dO > MAX_DIST || dS < SURF_DIST)
break;
}
return dO;
}
// 각 정점에서 노멀 벡터 계산
vec3 GetNormal(vec3 p)
{
float d = GetDist(p);
vec2 e = vec2(0.001, 0.0);
// x, y, z 좌표를 0.01씩 움직인 3개의 방향벡터로 각각 GetDist를 통해 해당 방향에 있는 물체의 정점까지 거리를 찾고,
// 이를 x, y, z 성분으로 사용한 노멀 벡터 생성
vec3 n = d - vec3(
GetDist(p - e.xyy),
GetDist(p - e.yxy),
GetDist(p - e.yyx)
);
return normalize(n);
}
// 각 정점에서 라이팅 계산
float GetLight(vec3 p)
{
vec3 L = normalize(g_lightPos - p);
vec3 N = GetNormal(p);
// Shade(Diffuse)
float dif = saturate( dot(N, L) );
// Shadow
// 물체 표면에서 광원을 향해 레이마칭하여 얻은 거리가
// 표면에서 광원까지의 거리보다 작다면,
// 그 사이에 또다른 물체의 표면이 가로막고 있다는 뜻이므로 이 표면에는 그림자가 생긴다.
// SURF_DIST만큼의 거리를 더해주는 이유 : 레이가 정점을 찾아내는 최소 거리(Threshold)이므로
// SURF_DIST에 1.0 초과 숫자를 곱해주는 이유 : 의도치 않은 음영이 생길 수 있으므로
float d = RayMarch(p + N * SURF_DIST * 2.0, L);
if(d < length(g_lightPos - p) )
dif *= 0.1;
return dif;
}
float DistLine(vec3 ro, vec3 rd, vec3 p)
{
return length(cross(p - ro, rd)) / length(rd);
}
/**************************************************************************************************
* Main
**************************************************************************************************/
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
// UV ================================================================================================
vec2 uv = fragCoord/iResolution.xy;
uv = (uv - 0.5) * vec2(iResolution.x/iResolution.y, 1.0) *2.0; // Square Area -1.0 ~ 1.0
float zoom = 1.3;
uv /= zoom;
vec2 mPos = iMouse.xy/iResolution.xy;
mPos = (mPos - 0.5) * vec2(iResolution.x/iResolution.y, 1.0) *2.0;
mPos /= zoom;
// Final Variables ===================================================================================
vec3 shp = vec3(0.0); // Shapes
vec3 col = vec3(0.0); // Colors of Shapes
// Ray Origin
vec3 ro = vec3(0.0, 1.1, 0.0);// + vec3(sin(mPos.x), 0., cos(mPos.x));
// Ray Direction : ro -> uv screen
vec3 rd = normalize(vec3(uv, 1.0));
float t = iTime;
float d; // Distance from point
vec3 p; // Result of RayMarching (3D Shapes)
float dif;// Diffuse
/*****************************************************************************************************************
* Body Start *
*****************************************************************************************************************/
g_lightPos += vec3(sin(t), 0., cos(t)) * 3.0;
d = RayMarch(ro, rd);
p = ro + rd * d;
dif = GetLight(p);
/*****************************************************************************************************************
* Body End *
*****************************************************************************************************************/
// Draw Shapes =======================================================================================
shp += dif;
// Apply Colors ======================================================================================
col += vec3(1.0, 1.0, 0.9);
// End Point =========================================================================================
fragColor.a = 1.0;
fragColor.rgb = shp * col;
}
유니티 엔진에서의 간단한 구현 예시
[1]

[2]
- 하나의 쉐이더 내에서 구현
- Cube Mesh에 쉐이더를 적용한다.

Raymarching.shader
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
// https://www.youtube.com/watch?v=S8AWd66hoCo
Shader "Rito/RayMarching"
{
Properties
{
[HideInInspector] _MainTex ("Texture", 2D) = "white" {}
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 100
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
#define MAX_STEPS 100
#define MAX_DIST 100
#define SURF_DIST 0.001
struct appdata
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f
{
float2 uv : TEXCOORD0;
float4 vertex : SV_POSITION;
float3 ro : TEXCOORD1;
float3 hitPos : TEXCOORD2;
};
sampler2D _MainTex;
float4 _MainTex_ST;
v2f vert (appdata v)
{
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
o.ro = mul(unity_WorldToObject, float4(_WorldSpaceCameraPos,1));
o.hitPos = v.vertex;
return o;
}
/*****************************************************************
Functions
******************************************************************/
// 트랜스폼의 회전 행렬 추출
float4x4 GetModelRotationMatrix()
{
float4x4 rotationMatrix;
vector sx = vector(unity_ObjectToWorld._m00, unity_ObjectToWorld._m10, unity_ObjectToWorld._m20, 0);
vector sy = vector(unity_ObjectToWorld._m01, unity_ObjectToWorld._m11, unity_ObjectToWorld._m21, 0);
vector sz = vector(unity_ObjectToWorld._m02, unity_ObjectToWorld._m12, unity_ObjectToWorld._m22, 0);
float scaleX = length(sx);
float scaleY = length(sy);
float scaleZ = length(sz);
rotationMatrix[0] = float4(unity_ObjectToWorld._m00 / scaleX, unity_ObjectToWorld._m01 / scaleY, unity_ObjectToWorld._m02 / scaleZ, 0);
rotationMatrix[1] = float4(unity_ObjectToWorld._m10 / scaleX, unity_ObjectToWorld._m11 / scaleY, unity_ObjectToWorld._m12 / scaleZ, 0);
rotationMatrix[2] = float4(unity_ObjectToWorld._m20 / scaleX, unity_ObjectToWorld._m21 / scaleY, unity_ObjectToWorld._m22 / scaleZ, 0);
rotationMatrix[3] = float4(0, 0, 0, 1);
return rotationMatrix;
}
// 위치 벡터 회전
float3 RotatePosObjectToWorld(float4x4 rotationMatrix, float3 pos)
{
return mul(rotationMatrix, pos).xyz;
}
float3 RotatePosWorldToObject(float4x4 rotationMatrix, float3 pos)
{
return mul(pos, rotationMatrix).xyz;
}
// 방향 벡터 회전
float3 RotateDirObjectToWorld(float4x4 rotationMatrix, float3 dir)
{
return mul((float3x3)rotationMatrix, dir);
}
float3 RotateDirWorldToObject(float4x4 rotationMatrix, float3 dir)
{
return mul(dir, (float3x3)rotationMatrix);
}
/*****************************************************************
Signed Distance Functions
******************************************************************/
float SdSphere(float3 p, float3 pos, float radius)
{
return length(p - pos) - radius;
}
float SdSphere2(float3 p, float3 pos, float radius, float3 scale)
{
p -= pos;
p /= scale;
p += pos;
return length(p - pos) - radius;
}
float SdTorus(float3 p, float3 pos, float radius, float width)
{
p = p - pos;
float r = radius;
float w = width;
float2 q = float2(length(p.xz) - r, p.y);
return length(q) - w;
}
float SdBox(float3 p, float3 pos, float3 size)
{
float3 q = abs(p - pos) - size;
return length(max(q, 0.0)) + min( max(q.x, max(q.y,q.z) ), 0.0);
}
/*****************************************************************
Operator Functions
******************************************************************/
float2x2 GetRotationMatrix2x2(float degree)
{
float radian = radians(degree);
float s = sin(radian);
float c = cos(radian);
return float2x2(c, -s, s, c);
}
float3 RotateX(float3 p, float3 pos, float degree)
{
p -= pos;
p.yz = mul(GetRotationMatrix2x2(degree), p.yz);
p += pos;
return p;
}
float3 RotateY(float3 p, float3 pos, float degree)
{
p -= pos;
p.xz = mul(GetRotationMatrix2x2(degree), p.xz);
p += pos;
return p;
}
float3 RotateZ(float3 p, float3 pos, float degree)
{
p -= pos;
p.xy = mul(GetRotationMatrix2x2(degree), p.xy);
p += pos;
return p;
}
float3 Scale(float3 p, float3 pos, float3 scale)
{
p -= pos;
p /= scale;
p += pos;
return p;
}
// Polynomial smooth min (k = 0.1);
float smin(float a, float b, float k)
{
float h = saturate(0.5 + 0.5 * (b - a) / k);
return lerp(b, a, h) - k * h * (1.0 - h);
}
float smin(float a, float b)
{
return smin(a, b, 0.2);
}
float3 Displacement(float3 p, float dist, float intensity)
{
float3 disp = sin(p * dist) * intensity;
return p + disp;
}
/*****************************************************************
Ray Marching Functions
******************************************************************/
// Sphere + Torus + Sphere*8
float SunShape(float3 p)
{
float t = _Time.y;
float3 centerPos = float3(-1.0, 0, 2.0);
float torus = SdTorus(RotateX(p, centerPos, 90), centerPos, 0.5, 0.1);
float s1 = SdSphere(p, centerPos, 0.3 + sin(t * 3.0) * 0.1);
float d = smin(torus, s1);
float3 s2_pos = centerPos; s2_pos.y += 0.9;
for(int i = 0; i < 8; i++)
{
float3 s2_p = RotateZ(p, centerPos, 45.0 * (float)i + t * 50.0);
float s2 = SdSphere2(s2_p, s2_pos, 0.1, float3(1.0, 2.0, 1.0));
d = smin(d, s2);
}
return d;
}
// Final SD Functions
float GetDist(float3 p)
{
float t = _Time.y;
float d = SunShape(p);
float3 pos2 = float3(1.0, 0, 2.0);
float scale = 0.7 + sin(t * 2.0) * 0.1;
float3 p2 = p;
p2 = RotateX(p2, pos2, t * 60.0);
p2 = RotateZ(p2, pos2, t * 90.0);
float box = SdBox(p2, pos2, scale);
float sp = SdSphere(p, pos2, scale * 1.3);
float d2 = max(box, -sp);
d = smin(d, d2, 0.4);
return d;
}
float3 GetNormal(float3 p)
{
float2 e = float2(0.01, 0);
float3 n = GetDist(p) - float3(
GetDist(p - e.xyy),
GetDist(p - e.yxy),
GetDist(p - e.yyx)
);
return normalize(n);
}
float GetLight(float3 N, float3 L)
{
return saturate(dot(N, L));
}
float Raymarch(float3 ro, float3 rd)
{
float dO = 0; // 누적 전진 거리
float dS; // 이번 스텝에서 전진할 거리
for(int i = 0; i < MAX_STEPS; i++)
{
float3 p = ro + dO * rd;
dS = GetDist(p);
dO += dS;
if(dS < SURF_DIST || dO > MAX_DIST)
break;
}
return dO;
}
/*****************************************************************
Fragment Function
******************************************************************/
fixed4 frag (v2f i) : SV_Target
{
float4x4 rotMatrix = GetModelRotationMatrix();
// Object Light Direction
float3 L = normalize(_WorldSpaceLightPos0.xyz);
L = RotateDirWorldToObject(rotMatrix, L);
float2 uv = i.uv - 0.5;
float3 ro = i.ro;
float3 rd = normalize(i.hitPos - ro);
float d = Raymarch(ro, rd);
fixed4 col = 0;
col.a = 1;
if(d < MAX_DIST)
{
float3 p = ro + rd * d;
float3 N = GetNormal(p);
col.rgb = GetLight(N, L);
}
else
discard;
return col;
}
ENDCG
}
}
}
장점
- 메시(Mesh) 데이터가 필요하지 않다.
- 부드러운 곡면이나 유체를 표현하기에 좋다.
- 반복되는 패턴을 렌더링하기에 좋다.
- 거리 함수, 연산 함수들을 이용하여 오브젝트들을 다양한 형태로 부드럽게 섞어 렌더링할 수 있다.
- 각 레이를 GPU 연산을 통해 병렬적으로 연산하기에 적합하다.
연관 개념
레이 트레이싱(Ray Traycing)
- 광원으로부터 나온 빛이 물체의 표면에 부딪히고, 그 다음 표면에 부딪히기를 반복해서 결국 카메라에 도달했을 때의 결과 색상을 화면에 출력하는 기법
- 현실적으로 모든 광선의 추적은 불가능하므로 역으로 카메라에서 픽셀마다 레이를 발사하여, 표면에 부딪힌 결과를 역연산하여 렌더링하는 방식을 사용한다.
- 기본적인 레이 트레이싱은 주로 반사/스페큘러 계산에 사용한다.
패스 트레이싱(Path Traycing)
- 레이 트레이싱의 일종
- 반사, 굴절이 없는 물체에도 모두 레이를 추적하여, 보다 현실적인 그래픽을 표현하는 기법
- 레이 트레이싱을 이용해 디퓨즈(Diffuse) 및 스페큘러(Specular), 전역 조명(GI, Global Illumination)을 주로 계산한다.