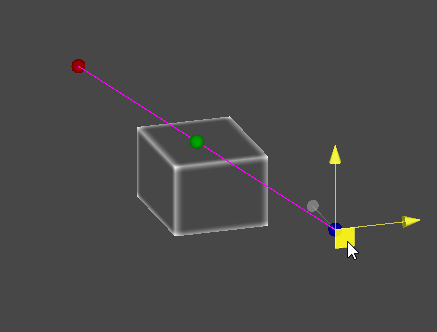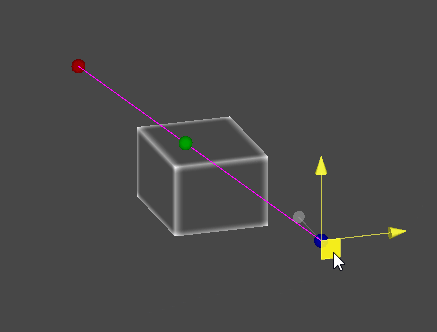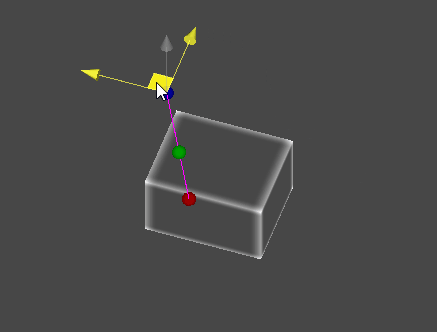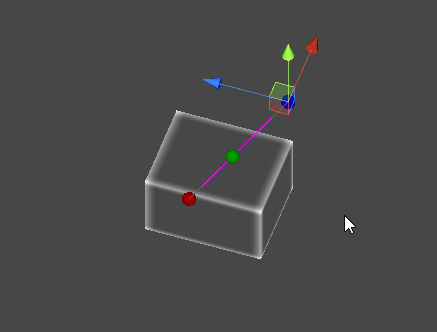
레이캐스트(Raycast)
- 공간 상의 한 점에서부터 목표 지점까지 가상의 광선을 발사하여, 광선에 닿는 물체의 표면을 검출한다.
AABB
-
Axis-Aligned Bounding Box
-
여섯 면이 모두 각각
X,Y,Z축에 정렬된 형태의 육면체 -
중심 좌표(
Vector3)와 각 축의 크기(Vector3) 또는
최소 좌표(Vector3)와 최대 좌표(Vector3)를 통해 정의할 수 있다.
Raycast to AAP
- AAP : Axis-Aligned Plane
육면체는 6개의 평면으로 이루어져 있다.
AABB 역시 6개의 평면으로 이루어져 있는데,
Axis-Aligned라는 특성 덕분에 각 평면에 대한 연산을 굉장히 간소화할 수 있다.
AABB는 각각 XY 평면, YZ 평면, XZ 평면에 평행한 평면 2개씩으로 이루어져 있다.
따라서 간소화된 세 가지 레이캐스트를 미리 구현하면 편리하다.
Raycast to XZ Plane
XY, YZ, XZ 평면 모두 연산은 동일하다.
그 중에서 예시로 XZ에 평행한 평면에 대한 레이캐스트,
즉 평면과 직선의 교점을 계산한다.
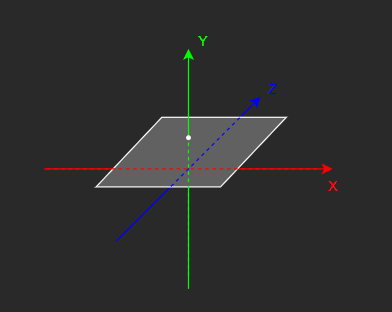
3D 공간에서 표현하면 위와 같다.
공간 상의 지점 A에서 B를 향한 레이캐스트를 표현해보면 다음과 같다.
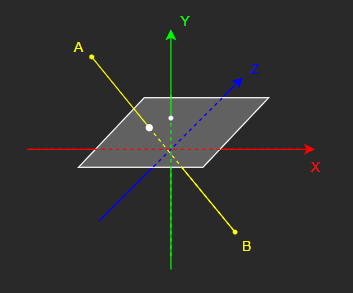
이를 다시 XZ 평면을 가로축으로, Y축을 세로축으로 하는 2D 평면 상에 표현해보면
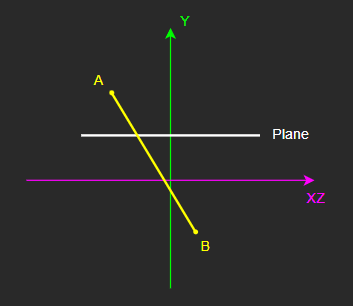
이렇게 되는데,
여기에 AB를 빗변으로 하는 삼각형을 그려볼 수 있다.
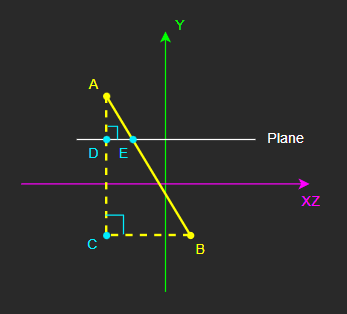
선분 AC는 Y축에 평행하다.
선분 BC, DE는 XY 평면에 평행하다.
삼각형 ABC는 직각삼각형이다.
그리고 삼각형 ADE 또한 직각삼각형이며, 삼각형 ABC와 닮은꼴이다.
따라서 이 성질을 이용해 AB와 Plane의 교차점인 E의 좌표를 구할 수 있다.
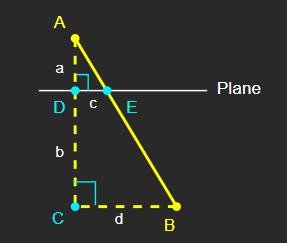
선분 AD의 길이를 a, CD의 길이를 b, DE의 길이를 c, BC의 길이를 d라고 정의할 때,
닮은꼴 삼각형의 성질에 따라 다음 비례식이 성립한다.
\[a : (a + b) = c : d\]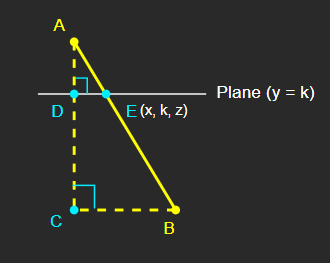
위의 평면은 XZ 평면에 평행하고, 이미 정보를 알고 있으므로 점 E의 y 좌표를 이미 알고 있는 셈이다.
따라서 평면을 y = k라고 정의할 때, 점 E의 좌표는 (x, k, z)와 같이 정의할 수 있다.
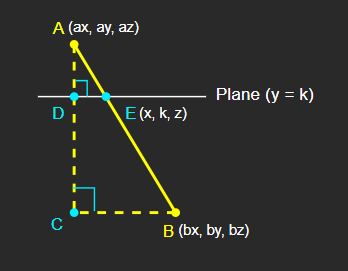
점 A, B의 좌표 역시 미리 알고 있다.
각각 (ax, ay, az), (bx, by, bz)라고 정의한다.
위에서 작성했던 비례식을 위의 좌표 값들을 이용해 바꾸어보면 다음과 같다.
c : d는 한 축이 아니라 x, z 축 모두에 대응하므로 각 축마다 비례식을 적용한다.
일단 첫 번째 비례식을 x에 대한 방정식으로 고친다.
같은 방식으로 z에 대한 방정식을 구할 수 있다.
x, z에 대한 각각의 방정식에서 공통된 부분이 있는데, 이를 r로 뽑아보면 다음과 같다.
그리고 x, z에 대한 방정식을 다시 정리해보면 다음과 같다.
따라서 위의 식을 이용해 XZ 평면에 평행한 평면과 직선 AB의 교점을 구할 수 있다.
일반화
XZ 평면에 평행한 평면에 대한 레이캐스트를 계산했다.
XY, YZ 평면에 평행한 평면들도 역시 방식은 동일하다.
알맞게 축만 바꾸어 방정식을 변경하면 된다.
Raycast to AABB
[1] 특징
AABB에 대한 레이캐스트는 결국 6개의 AAP에 대해 레이캐스트를 하는 것과 같다.
AABB와 직선 사이에 교점이 존재한다면, 교점은 하나 또는 두개일 수 있다.
만약 교점이 두 개 존재한다면, 둘 중 레이캐스트 시작점에 더 가까운 교점을 선택하면 된다.
[2] 평면 추려내기
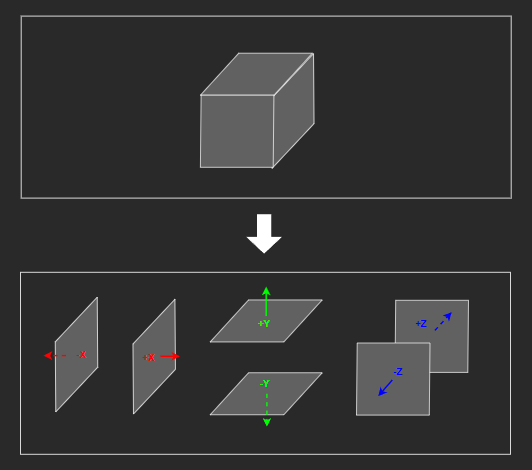
AABB의 여섯 평면은 두 개씩 서로 평행하다.
각 평면의 노멀 벡터를 이용해 평면을 지칭한다면,
+x 평면과 -x 평면은 평행하고, +y와 -y, +z와 -z 평면 역시 서로 평행하다.
점 A로부터 B로 레이캐스트를 할 때, 그 직선을 AB라고 한다.
직선 AB가 AABB와 교차하여 두 개의 교점이 존재한다면, 이 때 생기는 특징이 있다.
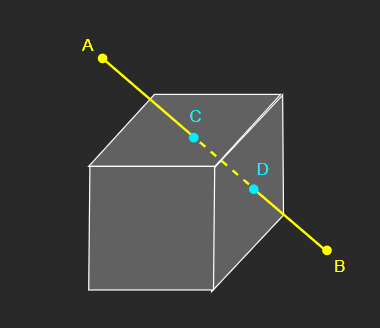
점 C는 +y 평면과 직선 AB의 교점이고, 두 교점 중 A에 더 가깝다.
점 D는 +x 평면과 직선 AB의 교점이고, 두 교점 중 B에 더 가깝다.
직선 AB의 벡터를 (a, b, c)라고 했을 때,
반드시 b <= 0이며, a >= 0이다.
여기서 점 D는 필요하지 않으므로 점 C만 고려한다.
명제를 만들어보면 다음과 같다.
1
2
직선 AB와 AABB가 두 교점에서 만날 때, 두 교점 중 점 A에 가까운 교점 C가 +y 평면에 있는 경우
직선 AB의 벡터 (a, b, c)에서 반드시 (b <= 0)이다.
그리고 한가지를 더 추론할 수 있다.
1
2
직선 AB와 AABB가 두 교점에서 만날 때, 두 교점 중 점 A에 가까운 교점 C가 +y 평면 또는 -y 평면에 있는 경우
직선 AB의 벡터 (a, b, c)에서 (b < 0)이면 점 C는 +y 평면에 있고 (b > 0)이면 점 C는 -y 평면에 있다.
위의 정보를 통해, 직선 AB의 벡터 (a, b, c)의 각 성분의 부호를 검사하여
교점이 존재할 수 있는 평면 후보를 6개에서 3개로 추려낼 수 있다.
a < 0이면 교점 C는 +x, -x 중에서 +x 평면에만 존재할 수 있고,
a > 0이면 교점 C는 +x, -x 중에서 -x 평면에만 존재할 수 있다.
b와 y, c와 z의 관계도 마찬가지다.
따라서 최대 세 개의 평면에 대해서만 레이캐스트를 수행하여
AABB에 대한 레이캐스트 결과(교점)를 알아낼 수 있다.
[3] 교점 검사하기
세 평면에 대한 레이캐스트를 차례로 수행했을 때,
얻은 좌표가 AABB의 평면 범위 내에 있는지 검사해야 한다.
예를 들어 XY(+z 또는 -z) 평면에 대한 레이캐스트를 수행했을 때 얻은 좌표 (x, y, z)에 대해,
AABB의 최소 지점, 최대 지점이 각각 (mx, my, mz), (Mx, My, Mz)라면
다음 조건식이 성립하면 좌표 (x, y, z)는 직선과 AABB의 교점이며,
따라서 AABB에 대한 레이캐스트의 결과 좌표일 것이다.
1
(mx <= x && x <= Mx) && (my <= y && y <= My)
z는 이미 XY 평면이 갖는 z 좌표와 동일하므로 검사할 필요가 없다.
마찬가지로 YZ(+x 또는 -x), XZ(+y 또는 -y) 평면에 대해서도
동일한 방식으로 레이캐스트를 수행하고 교점을 검사하여 최종 결과(좌표)를 얻어낼 수 있다.
구현 예시(Unity)
Struct Definition, Math Functions
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/// <summary> AABB의 최소 지점, 최대 지점 </summary>
private struct MinMax
{
public Vector3 min;
public Vector3 max;
public static MinMax FromBounds(in Bounds bounds)
{
MinMax mm = default;
mm.min = bounds.min;
mm.max = bounds.max;
return mm;
}
}
/// <summary> XY 평면에 정렬된 평면을 향해 레이캐스트 </summary>
private Vector3 RaycastToPlaneXY(in Vector3 A, in Vector3 B, float planeZ)
{
float ratio = (B.z - planeZ) / (B.z - A.z);
Vector3 C;
C.x = (A.x - B.x) * ratio + (B.x);
C.y = (A.y - B.y) * ratio + (B.y);
C.z = planeZ;
return C;
}
/// <summary> XZ 평면에 정렬된 평면을 향해 레이캐스트 </summary>
private Vector3 RaycastToPlaneXZ(in Vector3 A, in Vector3 B, float planeY)
{
float ratio = (B.y - planeY) / (B.y - A.y);
Vector3 C;
C.x = (A.x - B.x) * ratio + (B.x);
C.z = (A.z - B.z) * ratio + (B.z);
C.y = planeY;
return C;
}
/// <summary> YZ 평면에 정렬된 평면을 향해 레이캐스트 </summary>
private Vector3 RaycastToPlaneYZ(in Vector3 A, in Vector3 B, float planeX)
{
float ratio = (B.x - planeX) / (B.x - A.x);
Vector3 C;
C.y = (A.y - B.y) * ratio + (B.y);
C.z = (A.z - B.z) * ratio + (B.z);
C.x = planeX;
return C;
}
/// <summary> 값이 닫힌 범위 내에 있는지 검사 </summary>
private bool InRange(float value, float min, float max)
{
return min <= value && value <= max;
}
Raycast Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
private Vector3? RaycastToAABB(Vector3 origin, Vector3 end, in MinMax bounds)
{
ref Vector3 A = ref origin;
ref Vector3 B = ref end;
Vector3 min = bounds.min;
Vector3 max = bounds.max;
Vector3 AB = B - A;
Vector3 contact;
// [1] YZ 평면 검사
contact = RaycastToPlaneYZ(A, B, (AB.x > 0) ? min.x : max.x);
if (InRange(contact.y, min.y, max.y) && InRange(contact.z, min.z, max.z))
goto VALIDATE_DISTANCE;
// [2] XZ 평면 검사
contact = RaycastToPlaneXZ(A, B, (AB.y > 0) ? min.y : max.y);
if (InRange(contact.x, min.x, max.x) && InRange(contact.z, min.z, max.z))
goto VALIDATE_DISTANCE;
// [3] XY 평면 검사
contact = RaycastToPlaneXY(A, B, (AB.z > 0) ? min.z : max.z);
if (InRange(contact.x, min.x, max.x) && InRange(contact.y, min.y, max.y))
goto VALIDATE_DISTANCE;
// [4] No Contact Point
return null;
// 길이 검사 : 교점까지의 거리가 레이의 길이보다 더 긴 경우 제외
VALIDATE_DISTANCE:
float ab2 = AB.sqrMagnitude;
float len = (contact - A).sqrMagnitude;
return (ab2 < len) ? (Vector3?)null : contact;
}
Simplified Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 교점까지의 길이 검사를 배제한 간소화 메소드
private Vector3? RaycastToAABB_Simple(Vector3 origin, Vector3 end, in MinMax bounds)
{
ref Vector3 A = ref origin;
ref Vector3 B = ref end;
Vector3 min = bounds.min;
Vector3 max = bounds.max;
Vector3 AB = B - A;
Vector3 contact;
// [1] YZ 평면 검사
contact = RaycastToPlaneYZ(A, B, (AB.x > 0) ? min.x : max.x);
if (InRange(contact.y, min.y, max.y) && InRange(contact.z, min.z, max.z))
return contact;
// [2] XZ 평면 검사
contact = RaycastToPlaneXZ(A, B, (AB.y > 0) ? min.y : max.y);
if (InRange(contact.x, min.x, max.x) && InRange(contact.z, min.z, max.z))
return contact;
// [3] XY 평면 검사
contact = RaycastToPlaneXY(A, B, (AB.z > 0) ? min.z : max.z);
if (InRange(contact.x, min.x, max.x) && InRange(contact.y, min.y, max.y))
return contact;
// [4] No Contact Point
return null;
}
Gizmo Example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// MonoBehaviour Script
public Transform rayOrigin;
public Transform rayEnd;
public Transform cube;
private void OnDrawGizmos()
{
if (!rayOrigin || !rayEnd || !cube) return;
Bounds bounds = new Bounds(cube.position, cube.lossyScale);
MinMax minMax = MinMax.FromBounds(bounds);
Vector3 A = rayOrigin.position;
Vector3 B = rayEnd.position;
Vector3? contact = RaycastToAABB(A, B, minMax);
Gizmos.color = Color.red;
Gizmos.DrawSphere(A, 0.3f);
Gizmos.color = Color.blue;
Gizmos.DrawSphere(B, 0.3f);
Gizmos.color = Color.magenta;
Gizmos.DrawLine(A, B);
if (contact.HasValue)
{
Gizmos.color = Color.green;
Gizmos.DrawSphere(contact.Value, 0.3f);
}
}