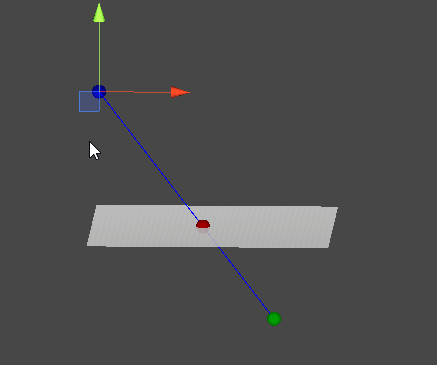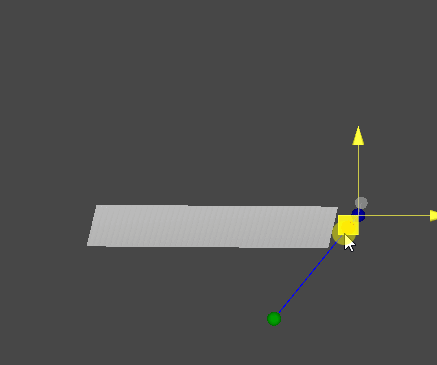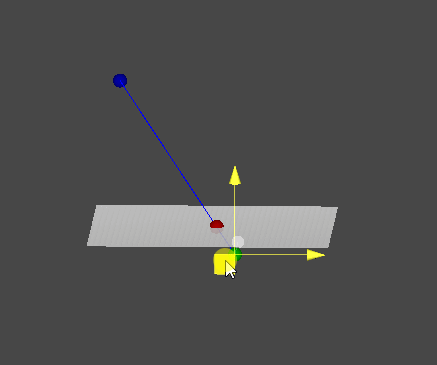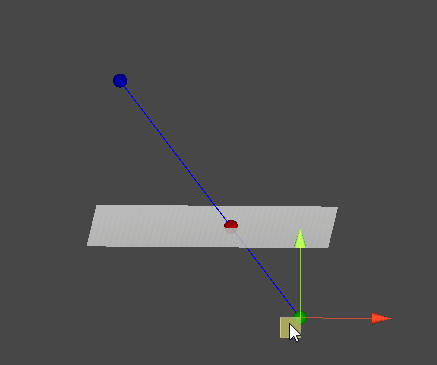
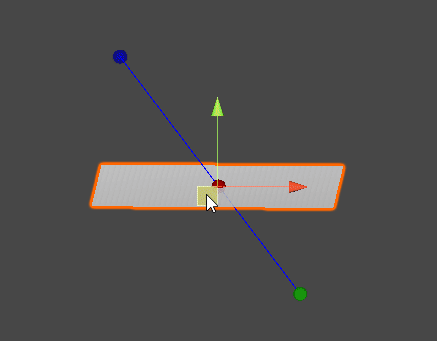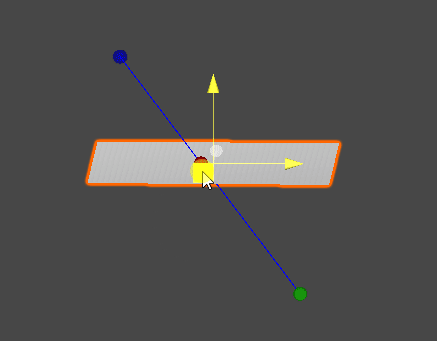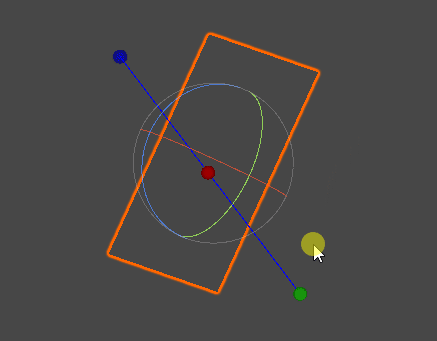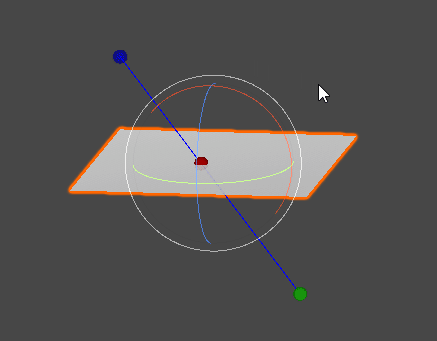
레이캐스트(Raycast)
- 공간 상의 한 점에서부터 목표 지점까지 가상의 광선을 발사하여, 광선에 닿는 물체의 표면을 검출한다.
평면(Plane)
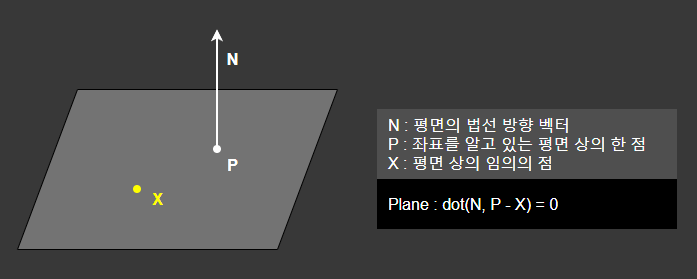
평면 위의 점 P와 평면의 법선 벡터 N을 알고 있으면 평면을 정의할 수 있으며,
평면 위의 임의의 점 X를 가정하여 dot(N, P - X) = 0을 통해 평면의 방정식을 정의할 수 있다.
직선과 평면의 접점 찾기
점 A와 점 B가 이루는 직선과 평면이 만나는 지점을 찾는다.
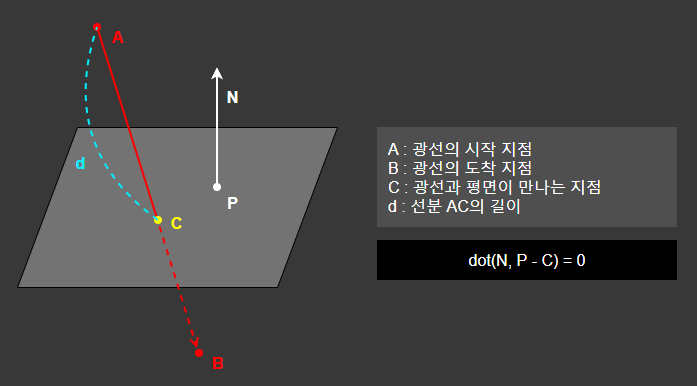
위와 같이 A, B, P, N이 주어졌을 때,
길이 d를 알아내고 이를 통해 직선과 평면의 접점 C를 알아내야 한다.
평면의 정의에 의해 다음과 같은 식을 얻을 수 있다.
\[dot(N, P - C) = 0\]그리고 내적의 분배 법칙에 의해
\[dot(N, P - C) = dot(N, P) - dot(N, C) = 0\]이며,
따라서
\[dot(N, P) = dot(N, C)\]이다.
# NOTE
내적의 분배법칙을 통해 유도하지 않더라도,
평면의 법선 벡터 N과 평면 위의 임의의 점 P에 대해
dot(N, P)는 항상 같은 값을 갖는 성질이 있다.
점 A에서 B를 향하는 직선의 방향 벡터를 nAB라고 할 때, 다음과 같이 구할 수 있다.
따라서 점 C는 다음과 같이 정의할 수 있다.
위에서 구한 식의 C에 대입하면
이며,
내적의 분배법칙에 의해
\[dot(N, P) = dot(N, A) + dot(N, nAB) * d\]이다.
위의 식을 내적의 결합법칙을 통해 정리하면 다음과 같다.
\[dot(N, P) - dot(N, A) = dot(N, nAB) * d\]따라서 점 C의 좌표는 다음과 같이 구할 수 있다.
구현 예시(Unity)
Raycast Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
private Vector3? RaycastToPlane(Vector3 origin, Vector3 end, Vector3 planePoint, Vector3 planeNormal)
{
ref Vector3 A = ref origin;
ref Vector3 B = ref end;
ref Vector3 P = ref planePoint;
ref Vector3 N = ref planeNormal;
Vector3 AB = (B - A);
Vector3 nAB = AB.normalized;
float d = Vector3.Dot(N, P - A) / Vector3.Dot(N, nAB);
// 레이 방향이 평면을 향하지 않는 경우
if (d < 0) return null;
Vector3 C = A + nAB * d;
float sqrAB = AB.sqrMagnitude;
float sqrAC = (C - A).sqrMagnitude;
// 레이가 짧아서 평면에 도달하지 못한 경우
if (sqrAB < sqrAC) return null;
return C;
}
Simplified Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 충돌 여부를 미리 알고 있는 경우 사용하는 간소화된 메소드
private Vector3 RaycastToPlane_Simple(Vector3 origin, Vector3 end, Vector3 planePoint, Vector3 planeNormal)
{
ref Vector3 A = ref origin;
ref Vector3 B = ref end;
ref Vector3 P = ref planePoint;
ref Vector3 N = ref planeNormal;
Vector3 AB = (B - A);
Vector3 nAB = AB.normalized;
float d = Vector3.Dot(N, P - A) / Vector3.Dot(N, nAB);
Vector3 C = A + nAB * d;
return C;
}
Gizmo Example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// MonoBehaviour Script
public Transform rayOrigin;
public Transform rayEnd;
public Transform plane;
public bool intersected;
private void OnDrawGizmos()
{
if (!rayOrigin || !rayEnd || !plane) return;
Vector3 ro = rayOrigin.position; // 레이 시작 지점
Vector3 re = rayEnd.position; // 레이 종료 지점
Vector3 pp = plane.position; // 평면 위치
Vector3 pn = plane.up; // 평면 노멀 벡터
Gizmos.color = Color.blue;
Gizmos.DrawSphere(ro, 0.3f);
Gizmos.DrawLine(ro, re);
Gizmos.color = Color.green;
Gizmos.DrawSphere(re, 0.3f);
Vector3? intersection = RaycastToPlane(ro, re, pp, pn);
intersected = (intersection != null);
if (intersected)
{
Gizmos.color = Color.red;
Gizmos.DrawSphere(intersection.Value, 0.3f);
}
}