Sphere
-
공간의 한 점에서부터 동일한 거리에 있는 점들의 집합
-
구체의 중심 좌표(
Vector3), 반지름(float)을 통해 정의할 수 있다.
AABB
-
Axis-Aligned Bounding Box
-
여섯 면이 모두 각각
X,Y,Z축에 정렬된 형태의 육면체 -
중심 좌표(
Vector3)와 각 축의 크기(Vector3) 또는
최소 좌표(Vector3)와 최대 좌표(Vector3)를 통해 정의할 수 있다.
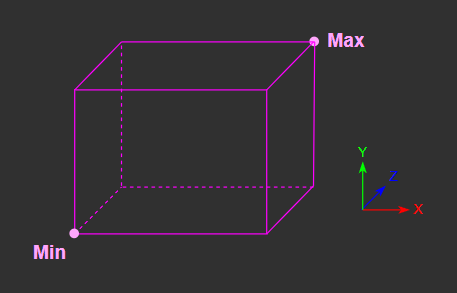
Closest Point to AABB
우선, AABB 바깥의 한 점에서부터
AABB 여섯 면 위의 가장 가까운 점을 찾는다.
2차원 평면의 예시는 다음과 같다.
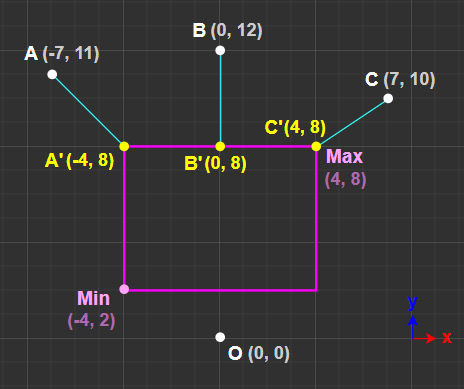
위의 그림에서 모든 노란색 점(Closest Point)들의 X 좌표만 살펴보자면,
Min.x보다 작은 점은 Min.x가 되고
Min.x와 Max.x 사이에 있는 점은 X 좌표가 유지되고
Max.x보다 큰 점은 Max.x가 된다.
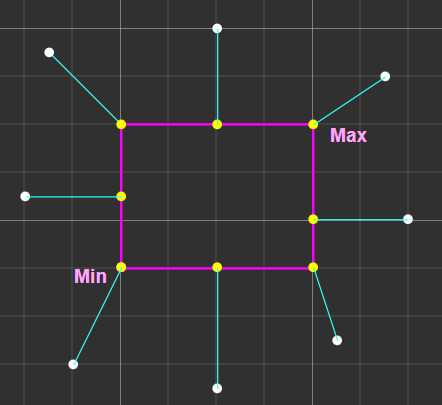
Y 좌표도 마찬가지로 Min.y, Max.y와의 관계를 따져보면 되고,
공간으로 확장해도 Z 좌표 역시 동일하다.
Unity C#으로 구현해보면 다음과 같다.
1
2
3
4
5
6
7
8
9
10
private Vector3 ClosestPointToAABB(Vector3 P, in AABB aabb)
{
if (P.x < aabb.min.x) P.x = aabb.min.x;
else if (P.x > aabb.max.x) P.x = aabb.max.x;
if (P.y < aabb.min.y) P.y = aabb.min.y;
else if (P.y > aabb.max.y) P.y = aabb.max.y;
if (P.z < aabb.min.z) P.z = aabb.min.z;
else if (P.z > aabb.max.z) P.z = aabb.max.z;
return P;
}
Sphere-AABB Intersection
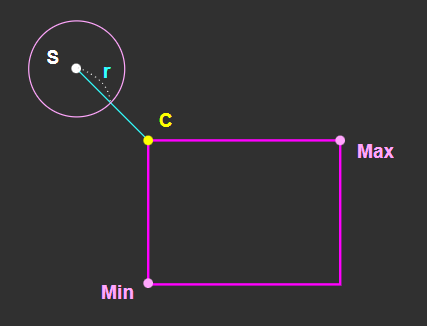
AABB 바깥에서 AABB로의 인접 지점을 찾았으면,
구체와 AABB의 교차 여부는 아주 간단히 확인할 수 있다.
점 S에서 C까지의 거리가 구체의 반지름인 r보다 작거나 같은지 확인하면 된다.
Unity C#으로 구현해보면 다음과 같다.
1
2
3
4
5
private bool SphereAABBIntersection(in Vector3 S, in float r, in AABB aabb)
{
Vector3 C = ClosestPointToAABB(S, aabb);
return (C - S).sqrMagnitude <= r * r;
}
벡터의 길이를 구하는 것은 항상 루트 계산을 동반한다.
하지만 두 벡터의 길이를 서로 비교하는 것은 굳이 루트를 씌우지 않고
제곱된 상태에서도 가능하며, 이렇게 하는 것이 더 저렴하다.
Example(Unity)
Methods
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
private struct AABB
{
public Vector3 min;
public Vector3 max;
public static AABB FromBounds(in Bounds b)
{
return new AABB { min = b.min, max = b.max };
}
}
/// <summary> 구체와 AABB의 교차 여부 확인 </summary>
private bool SphereAABBIntersection(in Vector3 S, in float r, in AABB aabb)
{
Vector3 C = ClosestPointToAABB(S, aabb);
return (C - S).sqrMagnitude <= r * r;
}
/// <summary> 한 점으로부터 AABB 위의 최단 지점 계산 </summary>
private Vector3 ClosestPointToAABB(Vector3 P, in AABB aabb)
{
if (P.x < aabb.min.x) P.x = aabb.min.x;
else if (P.x > aabb.max.x) P.x = aabb.max.x;
if (P.y < aabb.min.y) P.y = aabb.min.y;
else if (P.y > aabb.max.y) P.y = aabb.max.y;
if (P.z < aabb.min.z) P.z = aabb.min.z;
else if (P.z > aabb.max.z) P.z = aabb.max.z;
return P;
}
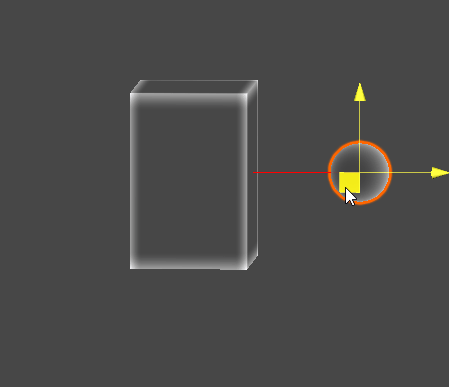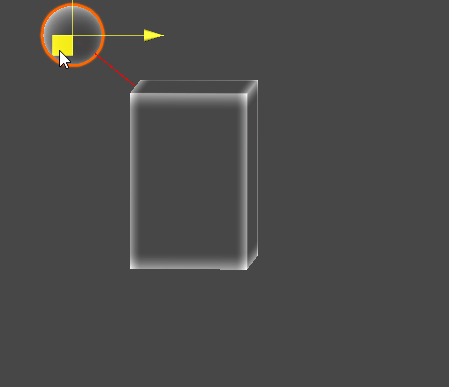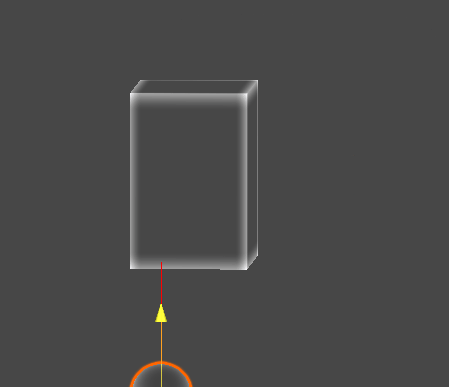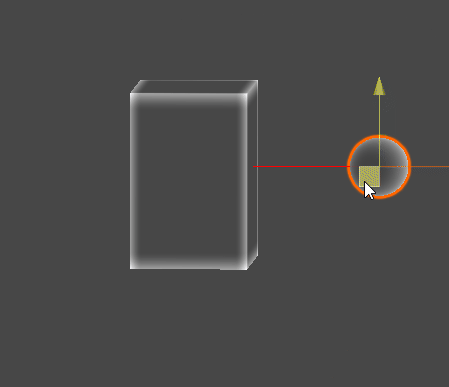
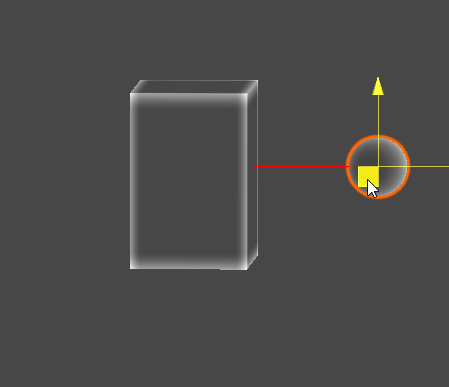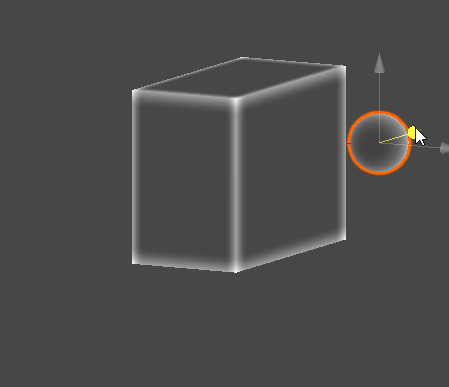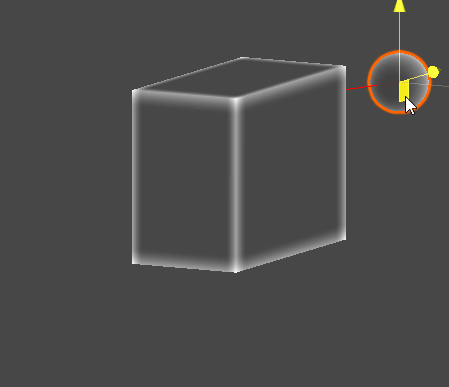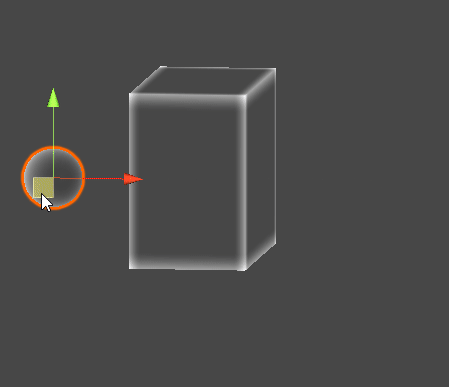
Gizmo Example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public Transform cube;
public Transform sphere;
public Mesh sphereMesh;
private void OnDrawGizmos()
{
if (!cube || !sphere) return;
Vector3 S = sphere.position;
float r = sphere.lossyScale.x * 0.5f;
Bounds b = new Bounds(cube.position, cube.lossyScale);
AABB aabb = AABB.FromBounds(b);
// Sphere - AABB 최단 지점
Vector3 C = ClosestPointToAABB(S, aabb);
Gizmos.color = Color.red;
Gizmos.DrawLine(S, C);
// Sphere - AABB 교차 검사
if (SphereAABBIntersection(S, r, aabb))
{
Gizmos.DrawSphere(C, 0.1f);
if (sphereMesh)
{
Gizmos.color = Color.yellow * 0.6f;
Gizmos.DrawMesh(sphereMesh, S, Quaternion.identity, sphere.lossyScale * 1.01f);
}
}
}