Sphere Cast
-
공간 상의 한 점에서부터 목표 지점까지 구체를 전진시켜, 구체 표면에 닿는 물체 표면을 검출한다.
-
레이캐스트와는 달리 구체의 반지름을 고려해야 한다.
Sphere Cast to Sphere
-
대상 물체가 구체인 경우에 대해서만 검사한다.
-
충돌 여부와 충돌 지점을 알아내는 것이 목표이다.
[1] 충돌 여부 판정
충돌 지점을 계산하기 전에, 우선 충돌 여부를 판정할 필요가 있다.
- A : 캐스트 시작 지점
- B : 캐스트 종료 지점
- S : 검사 대상 구체의 중심 위치
- r1 : 캐스트 구체의 반지름
- r2 : 구체 S의 반지름
- d : 점 S에서 직선 AB로 내린 수선의 길이
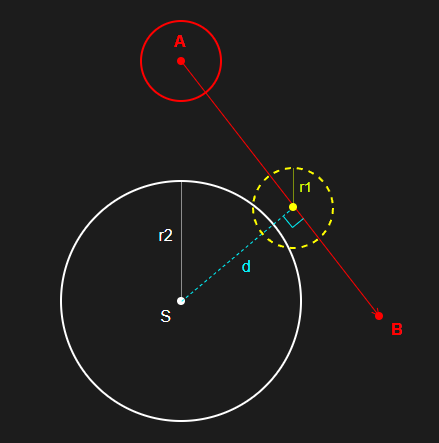
캡슐과 구체의 충돌을 판정하는 방식과 같다.
점 S에서 직선 AB로 수선의 발을 내렸을 때, 수선의 길이가 두 구체 반지름의 합보다 작거나 같으면 충돌로 판정된다.
수식으로 간단히 표현하면 다음과 같다.
\[d <= r1 + r2\][2] 충돌하는 순간의 구체 중심 위치 찾기
구체가 지점 A에서부터 B로 이동하다가 충돌하는 순간의 중심 위치를 C라고 했을 때,
이를 그림으로 그려보면 다음과 같다.
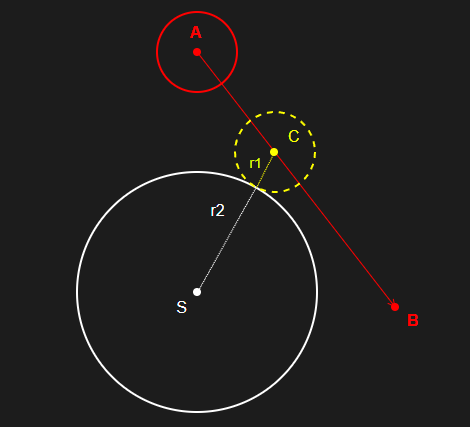
위 그림에서의 특징은 다음과 같다.
- 점 C는 직선 AB 위의 한 점이다.
- 선분 CS의 길이는
r1 + r2와 같다.
점 S에서 직선 AB로 내린 수선의 발을 D라고 했을 때, 그림으로 표현하면 다음과 같다.
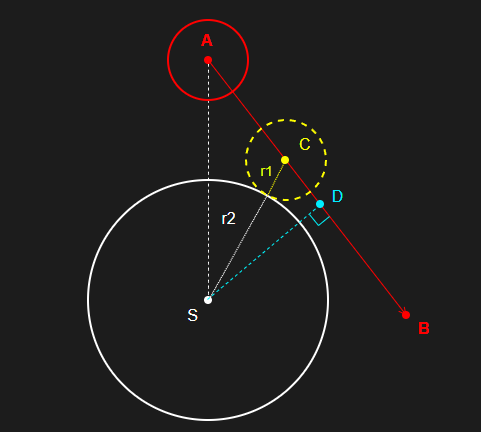
직선 AB는 이미 알고 있으므로 점 C의 좌표를 구하려면 선분 AC의 길이를 알아야 한다.
\[|AC| = |AD| - |CD|\]위의 식을 이용해 선분 AC의 길이 |AC|를 구할 수 있는데,
직선 AB의 방향 벡터를 nAB라고 했을 때
삼각형 ADS는 직각삼각형이므로 선분 AS를 nAB와 내적하면 |AD|를 구할 수 있다.
그리고 피타고라스 정리를 이용하여 |DS|의 길이를 구할 수 있다.
|CS| = r1 + r2로 이미 알고 있으므로, 마찬가지로 피타고라스의 정리를 이용하면 |CD|를 구할 수 있다.
이제 |AC|를 계산할 수 있으므로, 이를 통해 점 C의 좌표를 구할 수 있다.
하나의 식으로 정리해보면 다음과 같다.
\[C = A + nAB * ( dot(AS, nAB) - \sqrt{(r1 + r2)^{2} - |AS|^{2} + dot(AS, nAB)^{2}} )\][3] 충돌 표면 좌표 구하기
충돌 시의 구체 위치를 찾았으므로, 충돌 표면 좌표를 구하는 것은 간단하다.
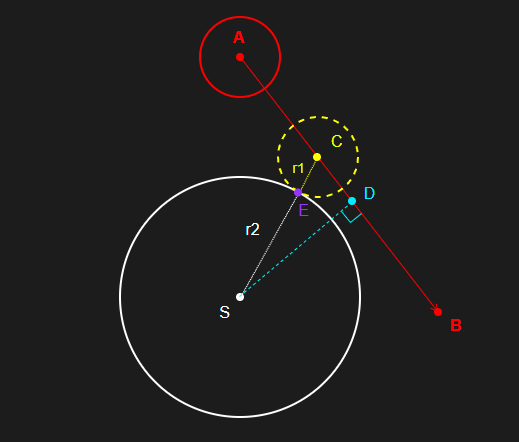
구하고자 하는 좌표를 E라고 할 때,
위의 식이 성립한다.
구현 예시(Unity)
Raycast Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
private Vector3? SphereCastToSphere(Vector3 origin, Vector3 end, Vector3 targetSphere, float castRadius, float targetRadius)
{
ref Vector3 A = ref origin;
ref Vector3 B = ref end;
ref Vector3 S = ref targetSphere;
ref float r1 = ref castRadius;
ref float r2 = ref targetRadius;
Vector3 AB = (B - A);
Vector3 nAB = AB.normalized;
Vector3 AS = (S - A);
float ab = AB.magnitude;
float as2 = AS.sqrMagnitude;
float as_ = Mathf.Sqrt(as2);
// 캐스트(A->B) 거리가 너무 가까운 경우
if (ab + r1 < as_ - r2) return null;
float ad = Vector3.Dot(AS, nAB);
// 캐스트 방향이 반대인 경우
if (ad < 0) return null;
float ad2 = ad * ad;
float ds2 = as2 - ad2;
float ds = Mathf.Sqrt(ds2);
float cs = r1 + r2;
// S에서 AB에 내린 수선의 길이가 두 구체의 반지름 합보다 긴 경우
if (ds > cs) return null;
float cs2 = cs * cs;
float cd = Mathf.Sqrt(cs2 - ds2);
float ac = ad - cd;
Vector3 C = A + nAB * ac; // 충돌 시 구체 중심 좌표
//Vector3 E = C + (S - C) * r1 / cs; // 충돌 지점 좌표
return C;
}
Simplified Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 충돌 여부를 미리 알고 있는 경우 사용하는 간소화된 메소드
private Vector3 SphereCastToSphere_Simple(Vector3 origin, Vector3 end, Vector3 targetSphere, float castRadius, float targetRadius)
{
ref Vector3 A = ref origin;
ref Vector3 B = ref end;
ref Vector3 S = ref targetSphere;
ref float r1 = ref castRadius;
ref float r2 = ref targetRadius;
Vector3 nAB = (B - A).normalized;
Vector3 AS = (S - A);
float as2 = AS.sqrMagnitude;
float ad = Vector3.Dot(AS, nAB);
float ad2 = ad * ad;
float ds2 = as2 - ad2;
float cs = r1 + r2;
float cs2 = cs * cs;
float cd = Mathf.Sqrt(cs2 - ds2);
float ac = ad - cd;
Vector3 C = A + nAB * ac; // 충돌 시 구체 중심 좌표
//Vector3 E = C + (S - C) * r1 / cs; // 충돌 지점 좌표
return C;
}
Gizmo Example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
// MonoBehaviour Script
public Mesh sphereMesh;
[Space]
public Transform castOrigin;
public Transform castEnd;
public float castRadius;
[Space]
public Transform targetSphere;
public float targetRadius;
private void OnDrawGizmos()
{
if (!castOrigin || !castEnd || !targetSphere || !sphereMesh) return;
Vector3 A = castOrigin.position;
Vector3 B = castEnd.position;
Vector3 S = targetSphere.position;
float r1 = castRadius;
float r2 = targetRadius;
Gizmos.color = Color.red * 0.8f;
Gizmos.DrawMesh(sphereMesh, A, Quaternion.identity, Vector3.one * 2f * r1);
Gizmos.DrawMesh(sphereMesh, B, Quaternion.identity, Vector3.one * 0.8f);
Gizmos.color = Color.blue * 0.8f;
Gizmos.DrawMesh(sphereMesh, S, Quaternion.identity, Vector3.one * 2f * r2);
Vector3? contact = SphereCastToSphere(A, B, S, r1, r2);
if (contact != null)
{
Gizmos.color = Color.yellow * 0.8f;
Gizmos.DrawMesh(sphereMesh, contact.Value, Quaternion.identity, Vector3.one * 2f * r1);
}
}

