기초 개념
기저 벡터(Basis Vector)
- n차원 공간에서 임의의 벡터를 표현할 수 있는, 선형 독립 관계의 벡터
- n차원 공간을 구성하려면 n개의 기저 벡터가 필요하다.
표준 기저 벡터(Standard Basis Vector)
- 기저 벡터 중에서도 원소 중 하나의 값이 1이고, 나머지 원소가 0인 벡터
- 예를 들어 2차원 평면에서의 표준 기저 벡터는
(1, 0),(0, 1)이다. - 공간의 축에 대응되는 벡터라고 할 수 있다.
공간 변환(Space Transformation)
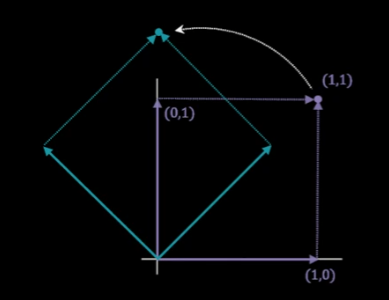
- 공간 변환이란 기존의 공간을 이루고 있던 표준기저벡터를 변경하여 새로운 공간을 만드는 작업이다.
- 이동, 회전, 크기 변환이 있다.
2차원 평면의 회전
2차원 회전 변환의 특징
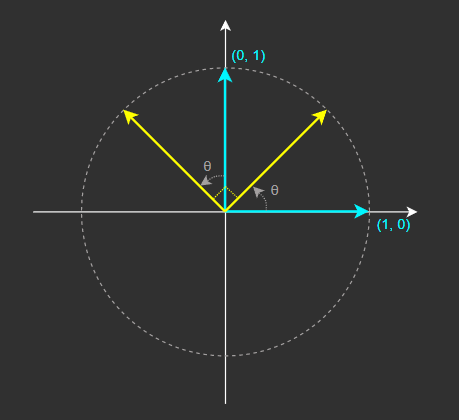
- 평면 내에서 반지름이 1인 원을 따라 기저 벡터들이 분포한다.
- 평면에서의 회전은 서로 직교하는 두 기저 벡터를 동일한 각도로 회전시켜 새로운 기저 벡터로 옮기는 것과 같다.
변환된 기저 벡터의 좌표
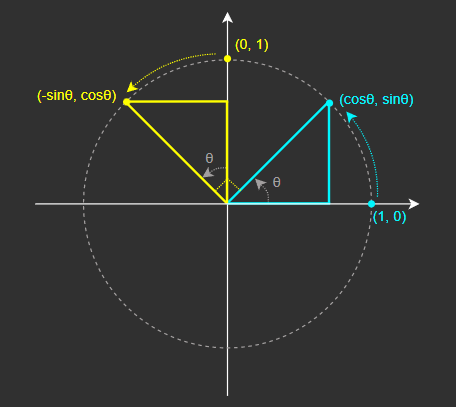
- X축 기저 벡터였던
(1, 0)은(cosθ, sinθ)로 옮겨진다. - Y축 기저 벡터였던
(0, 1)은(-sinθ, cosθ)로 옮겨진다.
변환 연산
변환 전의 임의의 좌표 (x, y)를 기저 벡터를 이용한 식으로 표현하자면 다음과 같다.
동일한 방식으로 변환 후의 좌표를 표현하면 다음과 같다.
\[\begin{flalign*} \quad \begin{matrix} (x', y') &=& x\,(cos\theta, sin\theta) + y\,(-sin\theta, cos\theta) \\ &=& (x\, cos\theta - y\, sin\theta, x\, sin\theta + y\, cos\theta) \end{matrix} && \end{flalign*}\]회전 행렬
위의 식을 행렬 연산으로 아래처럼 표현할 수 있고,
\[\begin{flalign*} \quad \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} cos\theta & -sin\theta \\ sin\theta & \,\,cos\theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} && \end{flalign*}\]따라서 2차원 평면의 회전 행렬은 다음과 같다.
\[\begin{flalign*} \quad \begin{pmatrix} cos\theta & -sin\theta \\ sin\theta & \,\,cos\theta \end{pmatrix} && \end{flalign*}\]3차원 공간의 회전
[1] 로드리게스 회전(축-각 회전)
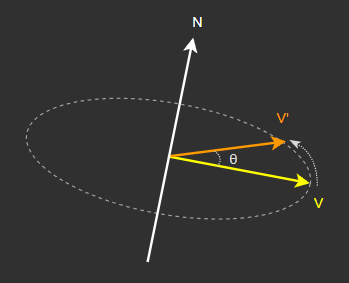
회전할 방향에 수직인 회전 축을 기준으로 회전한다.
회전하기 전의 벡터와 회전 이후 벡터는 하나의 평면을 이루며,
회전축은 이 평면의 법선 벡터와 같다.
N은 반드시 정규화된 벡터여야 한다.
- 로드리게스 회전 공식
구현 : 유니티 엔진
1
2
3
4
5
6
7
private void Rodrigues(ref Vector3 V, in Vector3 N, float radian)
{
float cos = Mathf.Cos(radian);
float sin = Mathf.Sin(radian);
V = (V * cos) + (1 - cos) * (Vector3.Dot(V, N)) * N + (Vector3.Cross(N, V) * sin);
}
단점
- 행렬로 변환하기 어렵기 때문에 렌더링 파이프라인 내에서 사용하기에 용이하지 않다.
[2] 오일러 회전
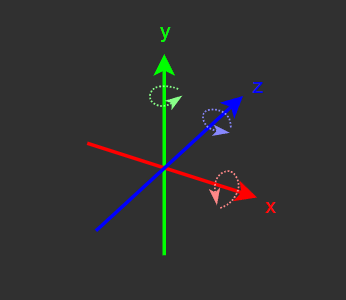
X축, Y축, Z축 회전을 각각 구성한다.
각각의 회전마다 2차원 평면에서의 회전 행렬을 유사하게 사용할 수 있다.
회전 각도를 표준화하여 표현하기에 아주 좋다는 장점이 있다.
회전 행렬
- X축 기준 회전 (YZ 평면 회전)
- Y축 기준 회전 (XZ 평면 회전)
- Z축 기준 회전 (XY 평면 회전)
문제점
각 축의 회전을 연달아 적용하므로,
동일한 회전이라도 회전 순서에 따라 결과가 바뀔 수 있으며
가장 큰 문제는, 이에 따라 짐벌락(Gimbal Lock) 현상이 발생한다는 것이다.
짐벌락(Gimbal Lock)
-
오일러 회전에서 두 회전 축이 완전히 겹치는 경우, 그 중 하나의 회전 축이 소실되는 현상
-
세 개의 축 중에서 두 번째로 적용되는 회전축이 문제를 일으킨다.
유니티 엔진의 예시
유니티 엔진에서 오일러 회전은 Z-X-Y 순서로 적용된다.
3개의 회전 기즈모 중 빨간색 기즈모는 로컬 X축 회전을 의미한다.
X축 회전이 정상적으로 적용되는 것을 확인할 수 있다.
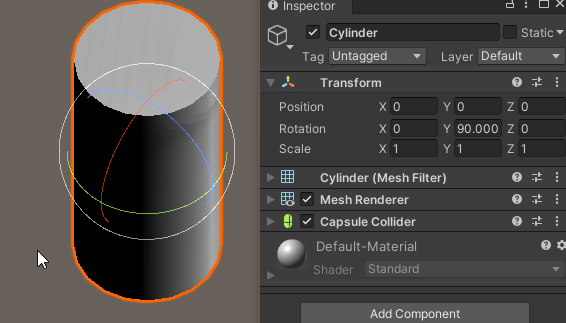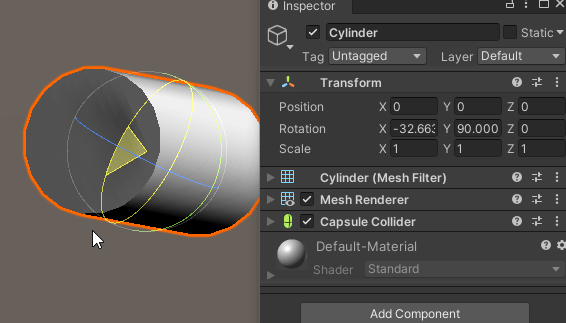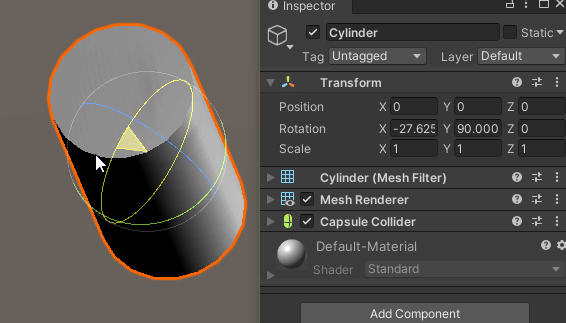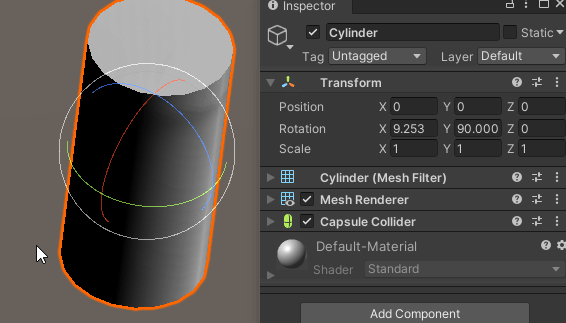
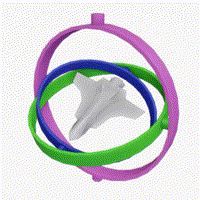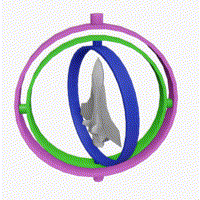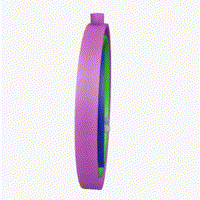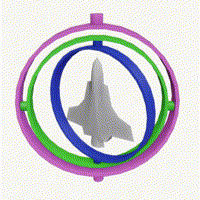
Y축 회전이 이미 90도로 적용되어 있는 상태에서도,
X축 회전이 정상적으로 적용된다.
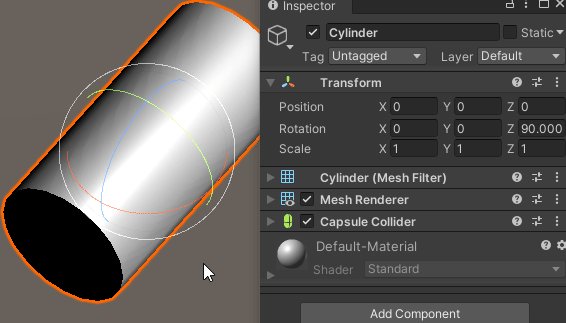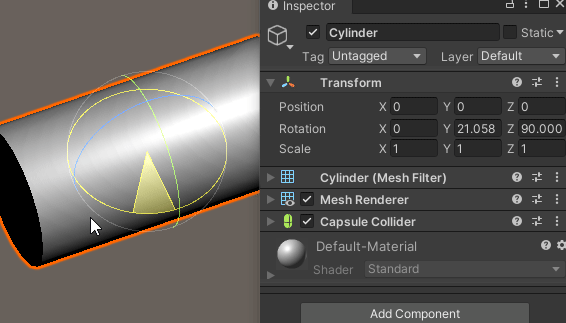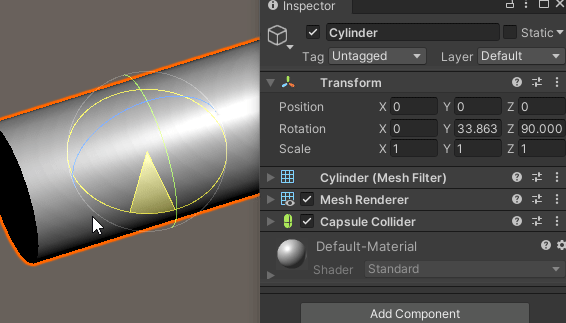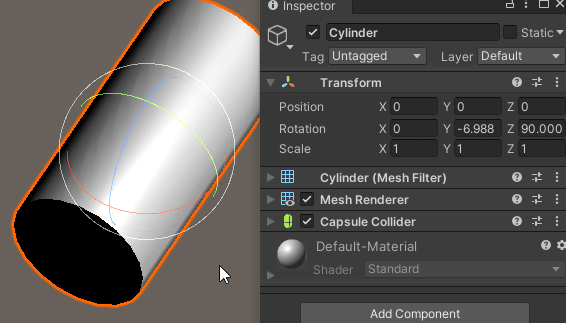
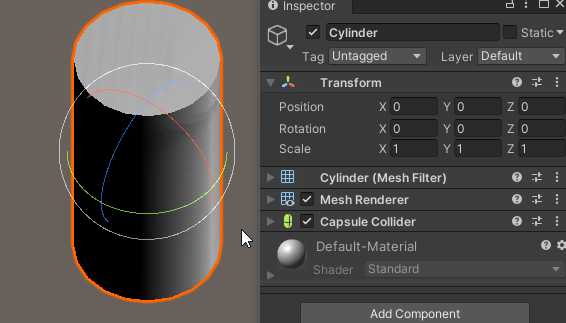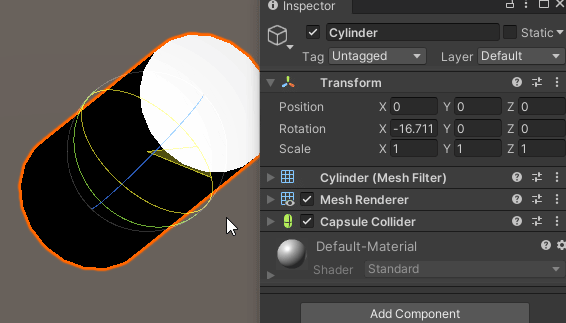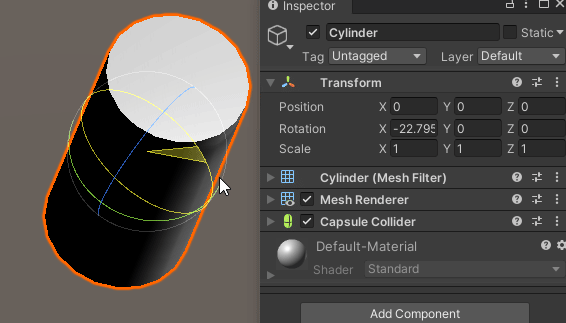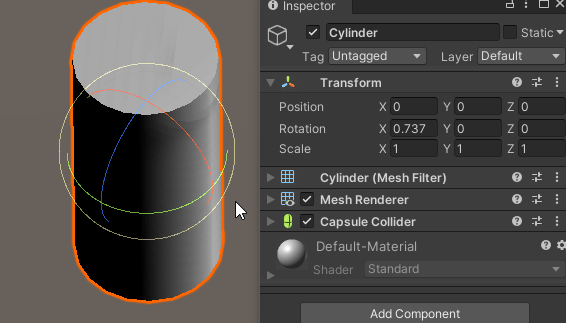
Z축 회전이 이미 적용되어 있는 경우,
X축으로 회전하면 문제가 발생한다.
분명 X축으로 회전을 시키는데도 불구하고 X축 회전값은 변하지 않고,
엉뚱하게 Y축 회전이 적용되는 것을 확인할 수 있다.
X축이 소실 되어버린 것이다.
해결 방법
3차원의 오일러 회전 내에서는 해결할 수 없고,
대신 이를 해결하기 위해 한 차원을 증가시켜
4차원의 연산을 통해 해결할 수 있는데,
여기서 사용되는 4차원의 수를 사원수(Quaternion)라고 한다.
복소수와 복소평면의 회전
복소수(Complex Number)
-
실수(Real Number)와 허수(Imaginary Number)의 합으로 표현되는 숫자
-
허수는 제곱하면
-1이 되는 숫자를 의미하며, 소문자i로 표기한다.
복소평면(Complex Plane)
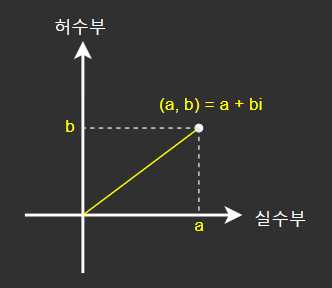
-
복소수를 실수부와 허수부로 나누어 2차원 평면에 표현한다.
-
평면의 X축을 실수부, Y축을 허수부로 정의한다.
-
복소평면의 좌표는 복소수(실수와 허수의 합)로 곧장 표현할 수 있다.
복소평면의 회전
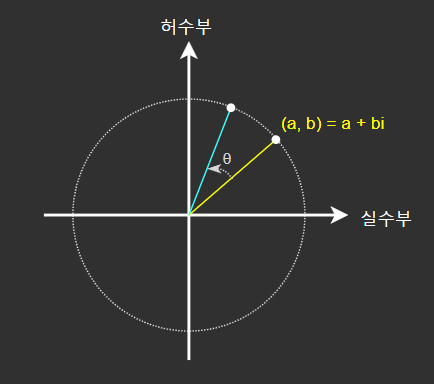
- 크기가 1인 복소수의 곱셈 연산은 평면에서의 회전에 대응된다.
Quaternion(사원수)
개념
-
3차원 벡터의 회전을 표현하기 위해, 한 차원 확장된 4차원으로 구성된다.
-
3개의 허수와 1개의 실수로 이루어져 있으며, 따라서 복소수로 표현될 수 있다.
-
3개의 원소로 이루어진 허수부는 벡터, 1개의 원소로 이루어진 실수부는 스칼라라고도 한다.
-
3차원 벡터에 대한 회전 정보를 담고 있다.
특징
-
짐벌락 현상이 발생하지 않는다.
-
4x4 행렬로 표현하기에 용이하다.
-
4차원 벡터의 길이는 언제나
1로 유지된다. ( \(\sqrt{x^2 + y^2 + z^2 + w^2} = 1\) ) -
\(ij = k\) , \(\quad jk = i\) , \(\quad ki = j\), \(\quad ijk = -1\)
연산의 특징
-
쿼터니언의 모든 원소의 부호가 바뀌어도 동일한 회전을 의미한다.
-
쿼터니언의 역함수(켤레 복소수)는 반대 방향의 회전을 의미한다.
-
쿼터니언에 쿼터니언을 곱하면
lhs만큼 회전시킨 후 변화한 표준 기저를 기준으로 다시rhs만큼 회전시키는 쿼터니언 값을 얻는다. -
쿼터니언끼리의 곱셈은 교환법칙이 성립하지 않는다.